Verrall: Expert Opinion

Study Strategy¶

Here is the content from the provided image formatted in Markdown with LaTeX for the mathematical formulas:

Checklist¶

My Notes¶

Actuarial judgement → Intervene in parameter selection. Why? Reasons include
- Internal policy changes → change in payment patterns
- Legislative changes → change in potential loss development
When can we incorporate expert opinion?
- Residuals in ODPB? → NO! Invalidates model assumptions
- CL → adjust LDFs → How does it affect/change the variance of losses? So variance is no longer valid
- \(\implies\) Use a Bayesian model. Why?
  - Allow incorporation naturally, without violation
  - Easy
  - Gives full distribution (not just mean/variance) of losses

Notation and Assumptions¶

\(C_{ij}\) → Incremental
\(D_{ij}\) → Cumulative
\(\lambda_{j}\) → LDF
\(M_{i}\) → expected losses = \(\text{ELR} \times\text{Premium}\)
\(y_{i}\) → incremental \% reported
Simplifying assumptions about data
- Triangular and,
- Fully Developed → No tail factors needed

Loss Distributions¶

Mack = Chain Ladder + Variance info
GLM¹
1. ODP
  - \(E(C_{ij}) =m_{ij}\) and \(\ln[m_{ij}]=\alpha_{i} + \beta_{i}\)
  - \(Var(C_{ij}) = \phi m_{ij}\)
  - Con → negative incremental values become a problem (log of negative number doesn't exist)
2. OD Negative Binomial
  - Same predictive distribution as ODP (reserve estimates and moments are identical)
    - But Correction to CL is apparent in the mean
  - \(E[D_{ij}|D_{i,j-1}, \lambda_{j}, \phi] = \lambda_{j}D_{i,j-1}\)
  - \(Var[D_{ij}|D_{i,j-1}, \lambda_{j},\phi]=\phi(\lambda_{j}-1)\lambda_{j}D_{i,j-1}\)
  - Pro → negative increments are not a problem
  - Con → if sum of column is negative \(\lambda_{j}\lt 1\) → variance negative
3. Normal
  - \(E[D_{ij}|D_{i,j-1},\lambda_{j},\phi] = \lambda_{j}D_{i,j-1}\)
  - \(Var[D_{ij}|D_{i,j-1},\lambda_{j},\phi]= \phi D_{i,j-1}\)
  - Pro → Can handle negative column sums too!

Markov Chain Monte Carlo (MCMC) methods¶

MCMC methods simulates one parameter at a time (conditional on values of other params) → creating a Markov chain where each param is considered in turn (instead of all at once)
Select prior for each parameter. Conditional distribution³. Combine these distributions → Posterior (to estimate future losses). Posterior is in between the prior distribution and the conditional distribution (data) spectrum.
Wide prior → SD is very large \(\implies\) Posterior → conditional distribution side of spectrum.
Narrow prior → SD small \(\implies\) Posterior → close to mean selected for prior distribution side of spectrum
SD \(\uparrow\) \(\implies\) closer to the conditional. SD \(\downarrow\) \(\implies\) closer to the prior mean

Prediction Error¶

\[ \text{Prediction Error} = \text{Process Variance} + \text{Estimation Variance} \]

or

\[ E[(y - \hat{y})^{2}] \]

Bayesian \(\gg\) Non-Bayesian¶

Non-Bayesian methods only calculate estimation variance (SE\(^{2}\))
Calculation of process variance is done separate and is complicated.
Bootstrap process → straightforward method to estimate process variance

Also, it produces the full distribution, including prediction error when run.

Large Standard deviation (wide priors ) \(\implies\) low confidence in parameters \(\implies\) larger prediction error.

Adjusting Bayesian Models with Expert Opinion¶

Insert expert opinion by selecting mean and SD of prior distribution
If no opinion → Wide prior (any mean)
If yes → set mean to our opinion and SD to how sure we are about it (more sure \(\implies\) smaller SD)
Opinion can be from a reserving actuary, or from claims leadership or underwriter (whoever has the expertise)

The Idea is important

The adjustments discussed are mere examples as to how expert opinion can be incorporated. The idea can be extended to other use cases / situations too!

Adjustment Type 1: Selecting Separate LDFs for each row¶

Standard CL → Same Dev factors for each row (varying by column) \(\lambda_{j}\)
But sometimes we need \(\lambda_{ij}\) that varies by both
Use negative binomial distribution
- Specify priors for LDFs
- Lean towards CL LDFs → Large SD
- Predetermined LDF → Small SD

Opinion: AY 4, 5, and 6 for Dev (2,3) should be 1.15

\[ \begin{align} \lambda_{ij} & = \lambda_{j}\ \forall\ i\ \text{and}\ j\neq 3 \\ \lambda_{i,3} & = \lambda_{3}\ \text{for } i = 1,2,3 \\ \lambda_{4,3} & = \lambda_{5,3} = \lambda_{6,3} \end{align} \]

\[ \text{Third Group} \sim \cdot(1.15, \text{small SD}) \]

The rest of the groups have mean 1 and infinite variance.

Adjustment Type 2: Only Use the Most recent \(N\) diagonals¶

Divide 6x6 triangle (full) data into two groups:
- \(\lambda_{ij}= \lambda_{j}\) for \(i = 7-j, 6-j, 5-j\)
- \(\lambda_{ij} = \lambda_{j}^*\) for \(i= 1,2,\dots,4-j\)

	1	2	3	4	5	6
1	*	*	*	\(\lambda_{4}\)	\(\lambda_{5}\)	\(\lambda_{6}\)
2	*	*	\(\lambda_{3}\)	\(\lambda_{4}\)	\(\lambda_{5}\)
3	*	\(\lambda_{2}\)	\(\lambda_{3}\)	\(\lambda_{4}\)
4	\(\lambda_{1}\)	\(\lambda_{2}\)	\(\lambda_{3}\)
5	\(\lambda_{1}\)	\(\lambda_{2}\)
6	\(\lambda_{1}\)

Give each set \(\lambda_{j}^*\) and \(\lambda_{j}\) → large variances so that they are estimated from data.
Then just use \(\lambda_{j}\) for future loss estimates (and not \(\lambda_{j}^*\))

A Bayesian Model for Bornhuetter-Ferguson¶

Incorporate expert opinion in ultimate loss estimate (not LDFs)
Expected loss in each row: \(M_{i}\) → Gamma distribution

\[ M_{i} = \dfrac{\alpha_{i}}{\beta_{i}} \qquad Var = \dfrac{\alpha_{i}}{\beta_{i}^{2}} = \dfrac{M_{i}}{\beta_{i}} \]

Set \(\alpha\) and \(\beta\) in such a way that the desired mean and variance are obtained. Decrease \(\beta\) to increase variance and adjust \(\alpha\) to keep the mean fixed \(M_{i} = 500\). So, the more we are sure about \(M\), the larger the \(\beta\) should be.

It's actually Benktander (cred weighting between B-F and Chain Ladder)

\[ E(C_{ij}) = Z_{ij} (\lambda_{j} - 1)D_{i,j-1} + (1-Z_{ij}) (\lambda_{j} - 1) M_{i} \dfrac{1}{\lambda_{j}\lambda_{j+1}\dots\lambda_{n}} \]

where,

\[ Z_{ij} = \dfrac{\sum_{k=1}^{j-1}y_{k}}{\beta_{i}\phi + \sum_{k=1}^{j-1} y_{k}} = \dfrac{\text{Cum \% reported}}{\text{Dispersion param} + \text{Cum \% reported}} \]

\(Z_{ij}\) → credibility factor. Cum % reported is the numerator.
\((\lambda_{j}-1)D_{i,j-1}\) → chain ladder estimate of incremental losses
\((\lambda_{j} - 1) M_{i} \dfrac{1}{\lambda_{j}\lambda_{j+1}\dots\lambda_{n}}\) → B-F estimate of incremental losses²

Work out an example

\(\alpha = 250\), \(\beta = 0.011\), \(\phi = 9.13\)
\(\lambda_{j} = [1.5, 1.2, 1.1, 1.0]\)
Compute BF estimate of incremental loss from 12 to 24 month maturity

More the \(\beta\), more confident we have in our a priori. We should adjust \(\alpha\) such that the expected value \(M_{i}\) remains the same.

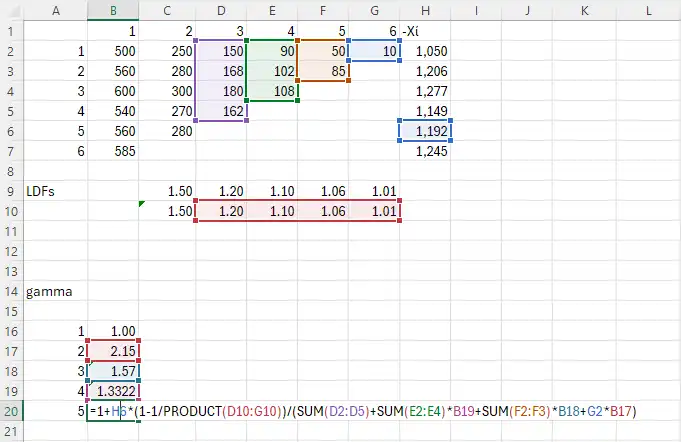
Estimating Row Parameters¶

Chain ladder estimates can be computed using row parameters, called \(\gamma_{i}\), rather than traditional LDFs.
Expected incremental losses are given by:

\[ E[C_{ij}| C_{1,j},C_{2,j},\dots,C_{i-1,j}, x, \phi] = (\gamma_{i}-1) \sum_{m=1}^{i-1}C_{mj} \]

or

\[ E(\text{incremental loss}) = (\text{row param} - 1) \times \sum_{\text{column}} \text{incremental losses} \]

Why use row parameters?

To create a fully stochastic model.
We first estimate column parameters (LDFs)
Use those to estimate row parameters

How to calculate \(\gamma_{i}\)?¶

Given,

\(\lambda_{j}\) → development factors
\(x_{i}\) → Expected ultimate losses

\[ \gamma_{1} = 1 \]

\[ \gamma_{2} = 1 + \dfrac{x_{2}(1-\dfrac{1}{\lambda_{n}})}{C_{1n}} \]

And for \(i=3,\dots,n\)

\[ \gamma_{i} = 1 + \dfrac{x_{i}\left( 1 - \dfrac{1}{\prod\limits_{k=n-i+2}^{n} \lambda_{k}} \right)}{\sum\limits_{m=1}^{i-1} c_{m,n-i+2} + \sum\limits_{k=n-i+3}^{n} \left[ \left( \prod\limits_{l=n-k+2}^{i-1} \gamma_{l} \right) \sum\limits_{m=n-k+2}^{n-k+1} c_{m,k} \right]} \]

Don't memorize

This is a daunting formula, you might make mistakes while memorizing the indices.
So instead, just try to understand the pattern of these calculations.

Expert Opinion incorporated

\(x_{i}\) is our prior distribution for our MCMC model
The \(\gamma\) will be our conditional distribution³
Smaller the SD → closer estimated losses would be to \(x_{i}\)

See how the next distribution solves the problem of the previous one. Understand the narrative ↩
Note that this formula is \((LDF-1)\times M_{i} \times \%\text{reported}\) ↩
Conditional → Driven by data! ↩↩