Testing the Assumptions of Age-to-Age Factors - Venter Factors

Study Strategy

• Tests are easy, just study them and treat them as an extension to what we did in the last paper (Mack Chainladder).
  • Only thing I'd suggest is to not spend too much time on the #Superiority of emergence pattern test ( 1) now and get to it only when you start practicing

Checklist

1. Know that under Mack's assumptions, the chain ladder method is the minimum variance unbiased linear estimator of future emergence
2. Be able to perform the different assumption tests, know if the data passes or fails the test, and know what assumption it's testing
   • Significance test
   • Superiority of emergence pattern test
   • Linearity test
   • Stability test
   • Correlation test
   • Diagonal dummy regression test
3. Be able to calculate \(f(d)\) and \(h(w)\) for the parameterized BF or Cape Cod methods for constant variance or variance proportional to loss
4. Understand how to calculate the number of parameters for a BF-CC emergence pattern
5. Be able to calculate expected ultimate losses using the additive chain ladder method

My Notes

Assumptions

1. Expected value of incremental losses in the next period \(\propto\) Losses to date
2. Losses are independent across AYs
3. The variance of the next incremental losses \(= f(\)cumulative losses to date\()\)

Tests

Significance test (#1)

Test

Are the loss dev factors (statistically) significant?

• constant = \(a\), factor = \(b\)
• Value of \(x > 2\times SD(x)\) \(\implies x\) is significant
• To prefer Chainladder: \(b\) should be significant but \(a\) should NOT be significant.

• What happens if \(a\) is also significant?

Superiority of emergence pattern test (#1)

Test

Is proportional emergence superior to other emergence patterns?

• Calculate \(\dfrac{SSE}{(n-p)^{2}}\) for different models.
  or AIC = \(SSE \times e^{ 2p/n }\) or BIC = \(SSE \times n^{p/n}\)

• Select the model with the lowest value.

Use incremental losses.

• Models to compare against
  1. Linear with constant \(y = b +ax\)
  2. Factor times parameter: \(y = f(d)h(w)\)

Linearity test (#1)

Test

Test for linearity (residuals vs losses to date should be random)

• Residuals should be random about zero (no patterns)
  • Should scatter randomly around zero
  • Magnitude should not change with time

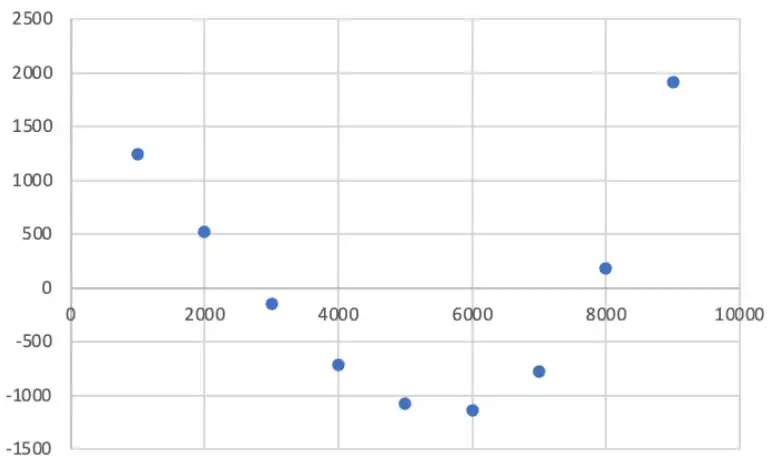
Here \(\downarrow\) we se a clear pattern in residuals \(\implies\) Fails the test, thus non-linear.

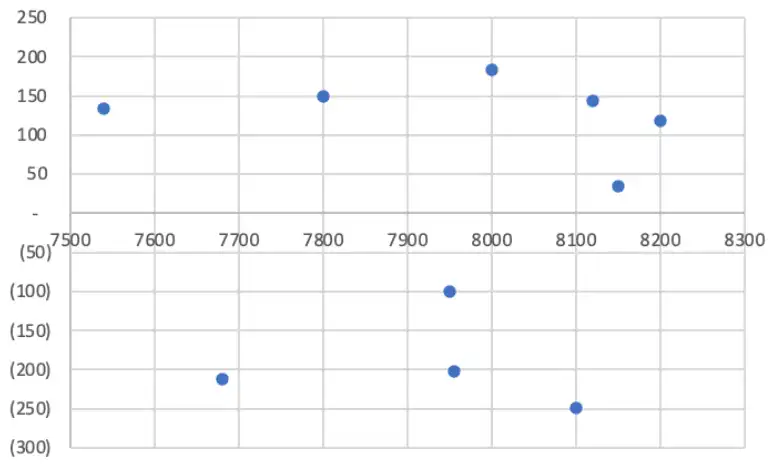
But here \(\downarrow\) the residuals look much more random \(\implies\) Passes linearity test

Stability test (#1)

Test

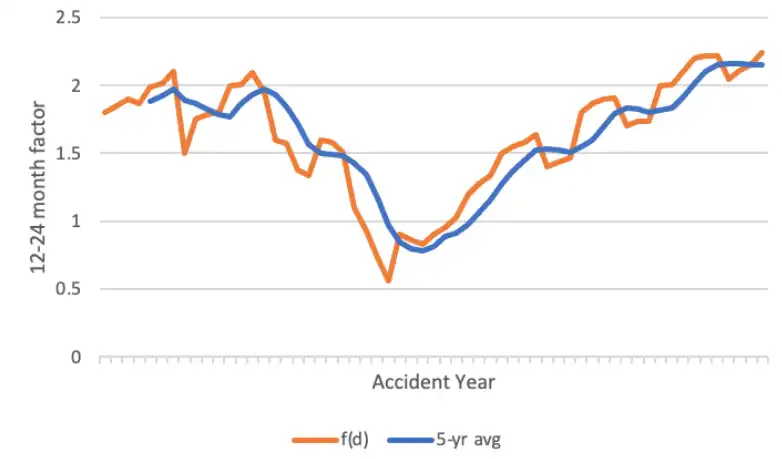
Are the development factors stable over time?

• LDF plotted against time
• 5-year average line should be relatively flat \(\implies\) factors are stable
• Trends in the LDFs \(\implies\) unstable,
  • try giving more weight to recent years

In this example \(\downarrow\) , the factors are not stable (the blue line is not flat)!

Other tests

1. Plot residuals against time (residuals should be random around 0)
2. Use a state-space model¹

Fix for a failing test?

• Use a weighted average with more weight on the more recent years
• Use a 5-year weighted average
• Use a 5-year simple average
• Use a 5-year ex hi/lo average
• Exclude the accident years where the age-to-age factors are lower
• Fit a curve to the age to age factors
• Use expert opinion to select the age-to-age factor
• Use industry data to select the age-to-age factor
• Adjust the triangle through the Berquist Sherman method
• Use the state-space model

Correlation test (#2)

Test

Correlation T-test to see if AY's are correlated. (unlike Spearman's rank test for development period correlation)

• Calculate \(f(w,d)\) - incremental factor
• Calculate sample correlation \(r\) (=correl)
• Calculate \(T = r\sqrt{ \dfrac{n-2}{1-r^{2}} }\)
• Test the hypothesis

Diagonal dummy regression test (#2)

Test

Diagonal dummy regression test

• \(y = \beta_{0} + \beta_{1}x + \beta_{2}d_{1} + \beta_{3}d_{2}\dots\)
• \(d_{j}=\begin{cases} 1, & \text{loss is in the j-th diagonal} \\ 0, & \text{otherwise}\end{cases}\)
• If any of the dummies, \(d_{j}\) are significant \(\implies\) Calendar year effects exist & Chain Ladder is inappropriate

Parameterized BF Method

BF-CC Emergence Pattern

Additive Chain Ladder

---

1. State-space model is a formal statistical model that measures the amount of instability around the current mean and the instability in the mean itself over time. ↩