Skip to content

Claims-made

Protip

Honestly, you just have to work with many problems related to claims-made to get a hang of it. No amount of reading will help you as much.

assets/images/2025/10/Claims-made-1760442680593.webp

Understanding

  • Retroactive date
  • Nose coverage
  • Tail coverage: Extended reporting endorsement

Gaps in Coverage

  • Professional switch: Occurrence \(\to\) CM
    • No gap as long as Occurrence expiry = Retroactive date
  • Professional switch: CM \(\to\) Occurrence
    • Gap since claims occurred in CM will not be covered post expiration.
    • So buy tail coverage that overlaps with the Occurrence
  • Professional retires:
    • Same situation
    • Buy tail coverage

Report year organization

You can make Report year development triangles as usual to know development in claims made policies.

  • RL = Report Lag
  • L(Reported in year, Report Lag)
RY RL 1 RL 2 RL 3 RL 4
2011 L(2011,0) L(2011,1) L(2011, 2) L(2011,3)
2012 L(2012,1)
2013 L(2013,2)
2014 L(2014,3)
  • The diagonal will be covered by Occurrence policy for AY2011
  • SIMPLE MENTAL MODEL
    • Think of a \(L(2012,1)\) as the accident occurred in 2012 - 1 = 2011, and was reported in 2012.

Principles of Claims-Made Pricing

P1: Price of CM vs Occurrence

  • Price of claims made policies \(\lt\) occurrence policies, as long as costs are increasing
  • More the time till settlement, more the cost of claims
  • Occurrence has report lag + settlement lag
  • CM has no report lag beyond the expiry of policy1
  • Occurrence covers claims reported in future years, more time for trends to impact the cost of those claims than for claims-made policies.
  • Answer why claims made rates are more accurate and responsive.
    • shorter forecast period for trends
    • trends are uncertain, applying to shorter periods reduce uncertainty \(\implies\) accurate
    • trend selections updated sooner because of shorter forecast period. \(\implies\) responsive

P3: Unexpected shifts in reporting patterns

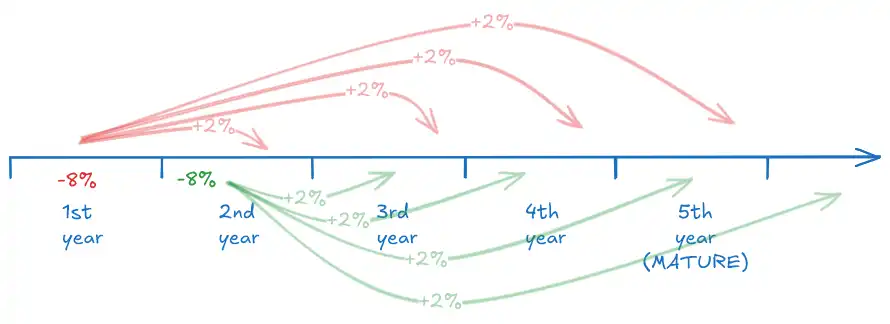
If there is a sudden unexpected shift in the reporting pattern, cost of a mature claims-made policy will be affected relatively little, if at all, relative to an occurrence policy.

assets/images/2025/10/Claims-made-1760088062304.webp

  • Assume the reporting pattern changes, 8% less reported from each year
    • -8% in the year (say, 1st year)
    • 2% of those unreported claims are reported in the next (2nd year) 🤖
    • 2% in the year after (3rd year) ⚒️
    • 2% (4th year)
    • 2% (5th year)
    • This distribution is shown by the red lines
  • The same happens for the 2nd year,
    • -8% distributed in the next years (green lines)
    • +2% (from 🤖)
    • So net change in reporting in the 2nd year = -6%, not as much as the first year
  • The same happens for the 3rd year
    • -8% distributed in the next years (as shown in the previous years)
    • +2% (from ⚒️ in first year)
    • +2% from the 2nd year
    • So net change in reporting in the 3rd year = -4%
  • Continue with this trend…
  • In the 5th year
    • -8%
    • But +8% from all the previous years…
    • net change = 0%

Reiterating it, if there is a sudden unexpected shift in the reporting pattern, cost of a mature claims-made policy will be affected relatively little, if at all, relative to an occurrence policy.

P4: No liability for pure IBNR, risk of reserve inadequacy is reduced greatly

  • CM only covered claims reported by the end of the policy term, don't have pure IBNR

P5: Investment income earned in CM is substantially less

compared to occurrence policies

  • No report lag beyond the end of the policy term1
  • less time than with occurrence policies for the premiums collected to be invested before claims are paid

  1. So note that, it's not like CM policies don't have report lag. There may be claims that occurred in the policy term that haven't been reported yet but the policy is still in-force, so there can be report lag within the policy term, but not beyond. ↩↩