Berquist-Sherman Techniques¶
Paid Losses Adjustment¶
Method¶
- Disposal rates
- Adjusted Paid claims using interpolation guided by disposal rates
The second step can be done in two ways:
Linear assumption¶
Assume claims and counts have a linear relationship
Use simple linear interpolation, say we found that the 24-mo adjusted paid count is higher than 24-mo (unadjusted) paid count. Then we must interpolate between 24-mo to 36-mo for the paid claims.
So, the 24-mo Adjusted claim is given by:
\[
\text{24-mo claim} + \dfrac{\text{Selected 24-mo DR} - \text{24-mo DR}}{\text{36-mo DR}- \text{24-mo DR}} \times(\text{36-mo claim} - \text{24-mo claim})
\]
- Easy to remember if you understand what is happening… we are just adding a portion of the difference \((\text{36-mo claim} - \text{24-mo claim})\)
- The portion is \(\dfrac{S-A}{B-A}\) where \(A \lt S \lt B\)
Exponential assumption¶
Assume claims and counts have an exponential relationship
- Find adjusted paid claim counts = paid counts \(\times\) latest Disposal rate for maturity
- Find the exponential fit i.e., \(\text{claims} = a\cdot \exp({b\times\text{counts}})\), we are going to find it for the interval "12-mo to 24-mo" (for an arbitrary AY)
\[
b_{\text{24-mo}} = \dfrac{\ln(\text{24-mo claim}) - \ln(\text{12-mo claim})}{\text{24-mo count}- \text{12-mo count}}
\]
Thus, \(b_{\text{24-mo}}\) is the fit between 12-mo and 24-mo. Note this convention for it will be needed to decide which parameters to use.
- For \(a\), just use the first relationship. So, \(a_{\text{24-mo}} =\dfrac{\text{24-mo claims}}{\exp(b_{\text{24-mo}} \times\text{24-mo counts})}\)
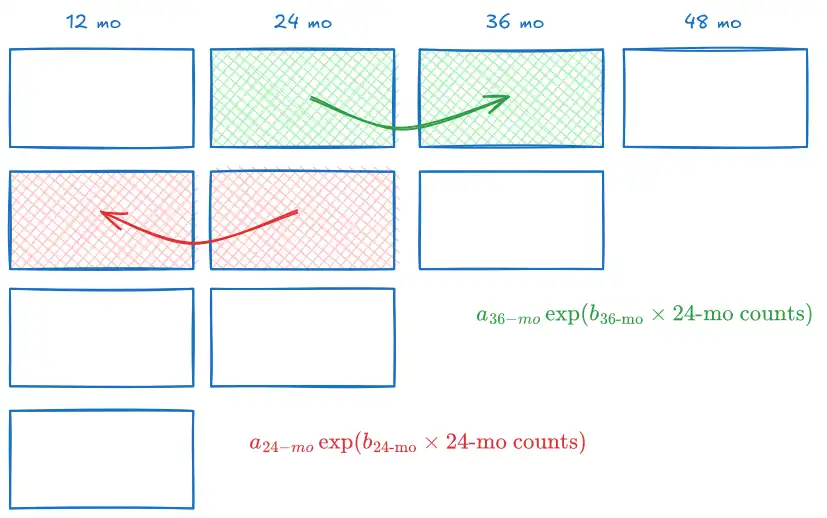
Now just apply the relationship to find \(\text{claims}= a \cdot \exp(b \times \text{counts})\) with the following logic (again, using 24-mo claims and counts as an example.)
- (GREEN) For 24-mo maturity, if the adjusted count \(\gt\) actual count, the adjusted claims should be \(\gt\) actual claims.
- Use the 24-mo to 36-mo relationship thus,
- adjusted claims = \(a_{36-mo}\exp(b_{\text{36-mo}}\times \text{24-mo counts})\)
- (RED) For 24-mo maturity, if the adjusted count \(\lt\) actual count, the adjusted claims should be \(\lt\) actual claims. So
- Use the 12-mo to 24-mo relationship thus,
- adjusted claims = \(a_{24-mo}\exp(b_{\text{24-mo}}\times \text{24-mo counts})\)
Case Reserve Adjustment¶
Method¶
- Find average case reserves (case severity) of the latest period
- Use paid severity trend to trend the the latest case severity \(\to\) Adjusted Average Case Severity
- Adjusted Cum rept claims = case severity \(\times\) open claim# + paid claims
Notes¶
- Detrend everything, even if it it inherently had the same trend as the Year-on-year losses
Misc.¶
- Medical malpractice:
- Cannot use paid loss data to estimate severity trends for CRAd
- Slow payment of claims for medical malpractice
- reduces data available by accident years to estimate paid severity at early maturities