Dynamic Adjustments - Cob-web Model

Revise

From Difference Equations we know that $y_t=a{y}_{t-1}+b$ has the solution,

$$y_t=\left(y_0-\frac{b}{1-a}\right)a^t+\frac{b}{1-a};b\ne 1$$

Let the demand function be $D_t=a{P}_t+b$ and, the supply function be $S_t=A{P}_{t-1}+B$.

For the equilibrium, $D_t=S_t$

$$\begin{array}{rl}a{P}_t+b& =A{P}_{t-1}+B\\ ⟹P_t& =\frac{A}{a}{P}_{t-1}+\left(\frac{B-b}{a}\right)\end{array}$$

which gives us the solution as

$$\begin{array}{rl}{P}_t& =\left(P_0-\frac{\frac{B-b}{a}}{1-\frac{A}{a}}\right){\left(\frac{A}{a}\right)}^t+\frac{\frac{B-b}{a}}{1-\frac{A}{a}}\\ P_t& =\left(P_0-\frac{B-b}{a-A}\right){\left(\frac{A}{a}\right)}^t+\frac{B-b}{a-A}\end{array}\text{\hspace{1em}(1)}$$

Suppose $P_e$ is the equilibrium price then,

$$\begin{array}{rl}a{P}_e+b& =A{P}_e+B\\ \therefore P_e& =\frac{B-b}{a-A}\end{array}\text{\hspace{1em}(2)}$$

From $(1)$ and $(2)$ we infer that,

$$\begin{array}{rl}{P}_t& =\left(P_0-P_e\right){\left(\frac{A}{a}\right)}^t+P_e\\ \therefore P_t-P_e& =\left(P_0-P_e\right){\left(\frac{A}{a}\right)}^t\end{array}\text{\hspace{1em}(3)(4)}$$

If the initial price is the equilibrium price (i.e. $P_0=P_e$), then there is no disturbance in equilibrium, thus we have dynamic stability.

If the initial price is not the equilibrium price ($P_0\ne P_e$) then $P_t\ne P_e$ and the difference is given by the equation

$$\boxed{P_t-P_e=\left(P_0-P_e\right){\left(\frac{A}{a}\right)}^t}$$

Now, let’s look at some cases

Case 1: Slope(supply) < Slope(demand)

Suppose $\left|\frac{A}{a}\right|<1$, then ${\left(\frac{A}{a}\right)}^t\to 0$ as $t\to \infty$.

Due to damped oscillation¹, there will be dynamic stability as $P_t$ will slowly converge to $P_e$.

Case 2: Slope(supply) > Slope(demand)

Suppose $\left|\frac{A}{a}\right|>1$, then ${\left(\frac{A}{a}\right)}^t\to \infty$ as $t\to \infty$.

This leads to explosive oscillation, and $\therefore$ this leads to unstable equilibrium.

Case 3: Slope(supply) = Slope(demand)

Suppose $\left|\frac{A}{a}\right|=1$, then ${\left(\frac{A}{a}\right)}^t\to 1$ as $t\to 1$.

The oscillation will be of equal magnitude and equilibrium will be unstable.

Refer to the Cob-web Market Model

S.No.	Case	Graph
$I$	$\Vert \frac{\delta }{\beta }\Vert <1$ $;\delta <\beta$.	Transclude of Cob-web-Market-Model-2024-09-25-09.41.32.excalidraw
$II$	$\Vert \frac{\delta }{\beta }\Vert >1$ $;\delta >\beta$.	Transclude of Cob-web-Market-Model-2024-09-25-09.53.29.excalidraw
$III$	$\Vert \frac{\delta }{\beta }\Vert =1$ $;\delta =\beta$.	Transclude of Cob-web-Market-Model-2024-09-25-09.54.56.excalidraw

Link to original

Conclusion

Thus only when $\frac{A}{a}<1$, in the first case, there will b dynamic stability. This model is called the Cob-web Market Model²

Footnotes

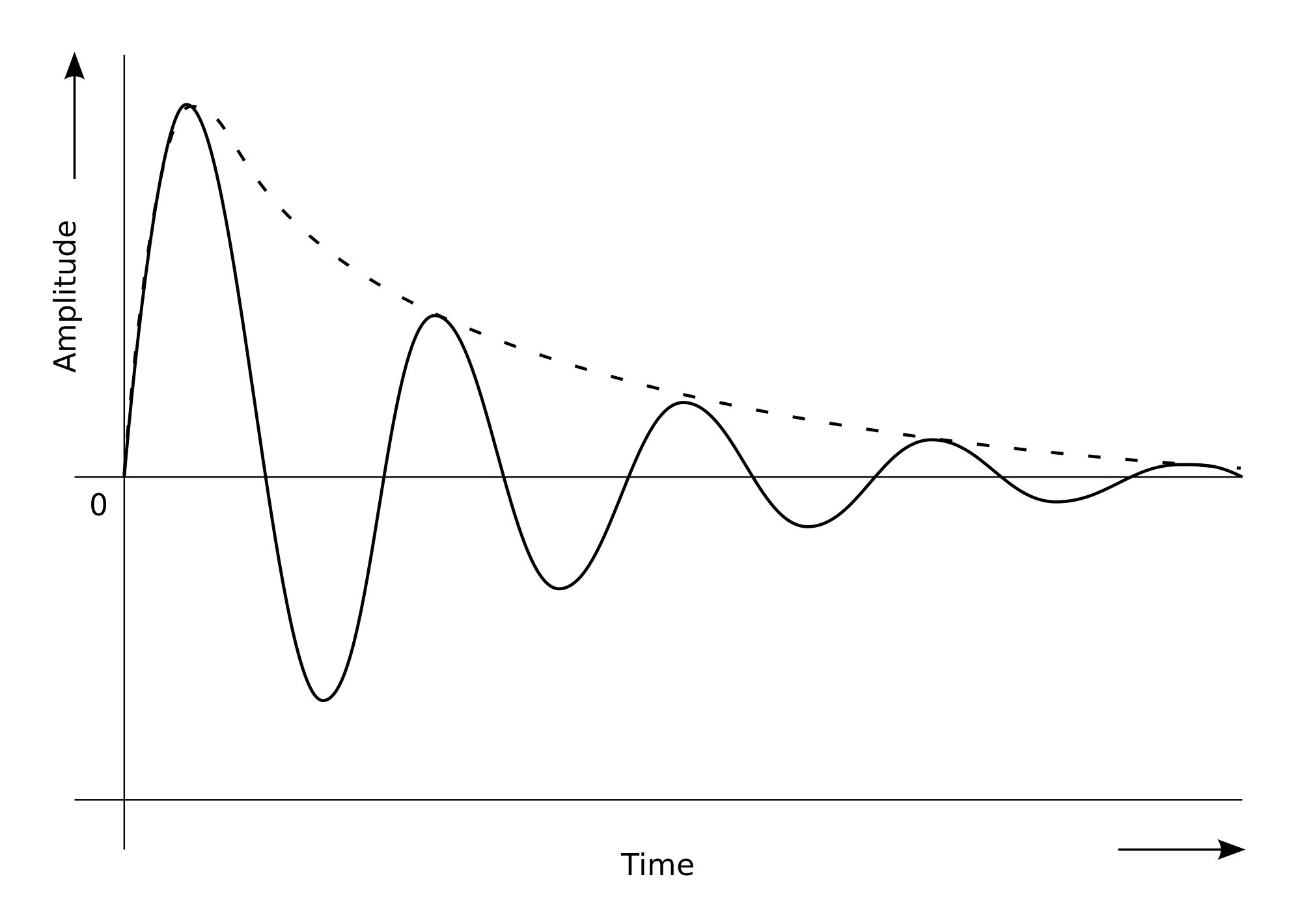1. Damped Oscillation ↩

2. Why is it called the cob-web model? That’s why. ↩