L59 Neural Networks for TS
- Artificial Neural Networks = simple mathematical models of the brain
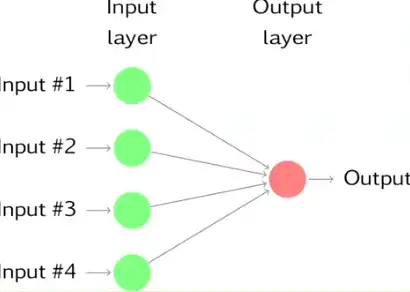
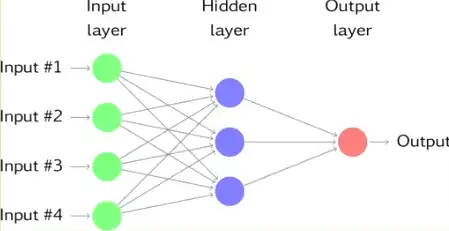
Network Architecture¶
- Network of neurons organized in layers
- Bottom layer: Predictors (inputs)
- Intermediate layers: "hidden neurons"
- Top layer: forecasts
- Loosely mimic the way our brain solves the problem
The "Perceptron"¶
- Network of nodes sending signals
- "Feed forward" network (one direction)
- A neuron connected with \(n\) other neurons and thus receives \(n\) inputs (\(x_{1,}x_{2},\dots,x_{n}\))
Weights¶
- Do you want to go to work?
- Weather? 0 or 1
- Weekday? 0 or 1
- We cannot tell the neural network these conditions, it learns them for itself
- It does so by applying weights
- A higher weight \(\implies\) the input is more important
- It computes weight form the data
Training in Perceptron¶
- For all inputs \(i\)
\[
W(i) = W(i) + a \times g'(\text{sum of inputs}) \times (T-A) \times P(i)
\]
- \(g'\) → derivative of the activation function
- \(a\) → learning rate
- \(P\) → Input vector
- \(T\) → Correct Output
- \(A\) → Output given by perceptron
Activation Function¶
- Mathematical equations
- Determine the output of NN layer given its inputs
- This is the secret ingredient that enables it to learn complex patterns in the data
Types of Activation Functions¶
- Sigmoid: \(f(x) = \dfrac{1}{1+e^{ -x }}\) for binary classification
- Tan-h: \(f(x) = \dfrac{e^{ x }-e^{ -x }}{e^{ x} + e^{ -x }}\) for hidden layer where output needs to be 0 centered
No Hidden Layers?¶
- Then the model reduces to a regression.
Extension¶
- Multilayer feed-forward
- The inputs to each node are combined using a weighted linear combination.
- More the number of hidden layers, the more complicated the neural network
Neural Network Autoregression (NNAR)¶
- lagged values of TS used as inputs
- only consider
- feed-forward networks
- one hidden layer
- \(NNAR(p,k)\)
- \(p\) lagged inputs
- \(k\) nodes in the hidden layer
- \(NNAR(p,0)\) is equivalent to \(AR(p)\)
Batch, Iterations & Epoch¶
- Big dataset (we cannot pass everything to the NN at once)
- divide datasets into "batches"
- Batch size is a hyper parameter
- Iterations it the number of batches needed to compute one epoch
- One Epoch = the ENTIRE dataset is passed forward and backward through the neural network only ONCE
Use of More Than one Epoch¶
- Use gradient descent to update weights
- As the # of epochs increases,
- the weights are changed in NN
- from Underfitting to Optimal to Overfitting