L24 Double and Triple Exponential Smoothing
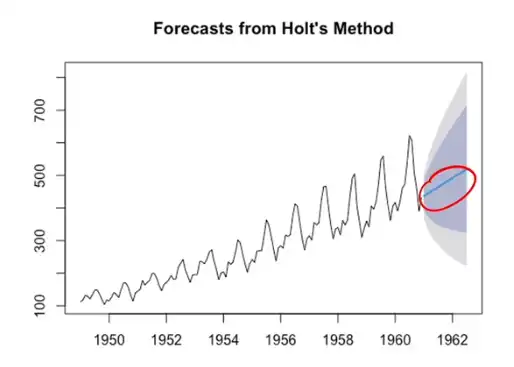
Double Exponential Smoothing (Holt's Method)¶
- When TS has
- linear trend
- no seasonal pattern
- aka Holt's trend corrected or SO Exponential smoothing
- Introduce a term, \(b_{t}\) to take care of trend
$$
s_{0} = y_{0}
$$
and for \(t\gt 0\)
\[
s_{t} = \alpha y_{t} + (1-\alpha)(s_{t-1} + b_{t-1})
\]
and
\[
b_{t} = \beta(s_{t}-s_{t-1}) + (1-\beta)b_{t-1}
\]
where,
- \(b_{t}\) is the best estimate of trend at \(t\)
- \(0 \lt \beta \lt 1\) is the trend smoothing factor
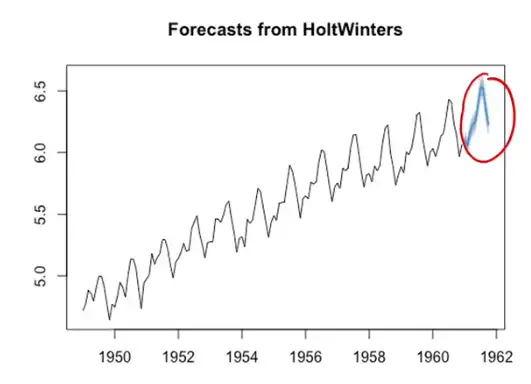
Triple Exponential Smoothing (Holt Winter's Method)¶
- Forecast the TS when data has
- Linear trend
- Seasonal pattern
- Involved notations
- \(s_{t}:\) smoothed statistic
- \(\alpha:\) smoothing or weighing param \((0,1)\)
- \(b_{t}:\) best estimate of trend
- \(\beta:\) trend smoothing factor \((0,1)\)
- \(c_{t}:\) sequence of seasonal correction factor
- \(\gamma:\) seasonal change smoothing factor \((0,1)\)
-
Further notations
- \(L\) = length of cycle of seasonal change. Monthly data → \(L=12\)
- \(N\) = number of cycles. For 10 years, \(N = 10\) (120 months)
-
Additive seasonality = seasonal effect is roughly constant over time
\[
Y_{t} = T_{t} + S_{t} + e_{t}
\]
- Multiplicative seasonality = larger seasonal fluctuations when time series is at a higher level
\[
Y_{t} = T_{t} \times S_{t} \times e_{t}
\]
Multiplicative Seasonality
\[
\begin{align}
s_{0} & = y_{0} \\
s_{t} & = \alpha \dfrac{y_{t}}{c_{t-L}} + (1-\alpha)(s_{t-1}+b_{t-1}) \\
b_{t} & = \beta(s_{t}-s_{t-1}) + (1-\beta)b_{t-1} \\
c_{t} & = \gamma \dfrac{y_{t}}{s_{t}} + (1-\gamma) c_{t-L}
\end{align}
\]
Additive Seasonality
\[
\begin{align}
s_{0} & = y_{0} \\
s_{t} & = \alpha + (y_{t} - c_{t-L}) + (1-\alpha)(s_{t-1}+b_{t-1}) \\
b_{t} & = \beta(s_{t} - s_{t-1}) + (1-\beta)b_{t-1} \\
c_{t} & = \gamma(y_{t} - s_{t-1} - b_{t-1}) + (1-\gamma) c_{t-L}
\end{align}
\]
Holt's Filtering (same as Smoothing) on the Data