Smoothing Techniques (SMA, EMA)¶

Smoothing techniques are essential for reducing noise—the random variations in a time series—to reveal the underlying trend and important patterns for better forecasting.

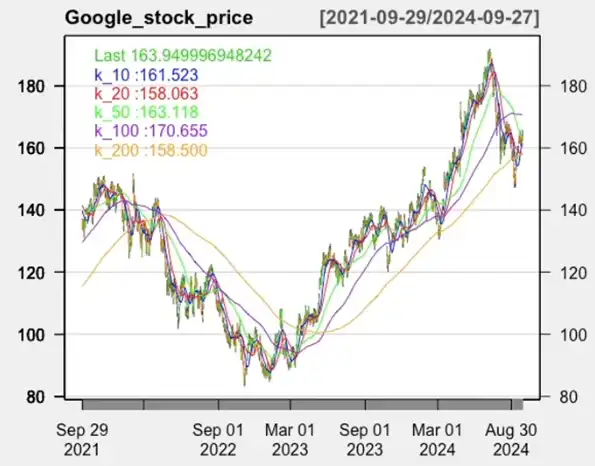
1. Simple Moving Average Smoothing (SMA)¶

The smoothed series is derived by taking the arithmetic average of the last $k$ (order) elements of the series.
$$S_{t} = \dfrac{Y_{t}+Y_{t-1} + \dots + Y_{t-k+1}}{k}$$

Order Influence: Increasing the order $k$ results in more significant smoothing of the data.

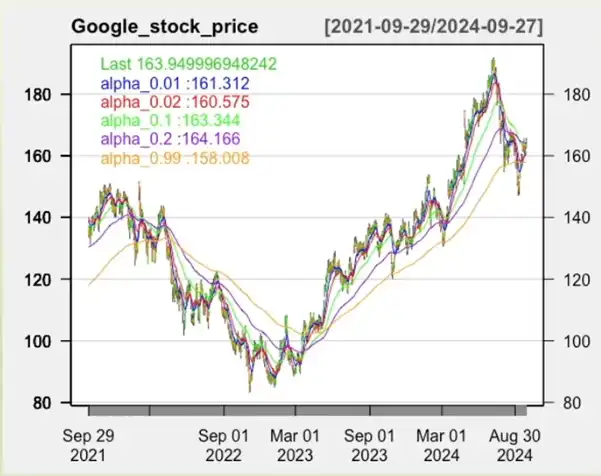
2. Exponential Smoothing (EMA)¶

Unlike SMA, Exponential Smoothing uses a weighted average where weights decrease exponentially as observations get older, placing more importance on recent data.

Mathematical Structure¶

Initialization: $S_{0} = Y_{0}$.
Recursive Formula: $S_{t} = \alpha Y_{t-1} + (1-\alpha)S_{t-1}$, where $0 < \alpha < 1$ is the smoothing factor.

Characteristics of $\alpha$¶

Low $\alpha$: Observations have lower influence; the model is less responsive to recent changes and results in more smoothing.
High $\alpha$: Reduces the effect of smoothing, making the model highly sensitive to recent data points.

Forecast Representation¶

The current smoothed value serves as the forecast for the next period ($S_{t} = \hat{Y}_{t+1}$), leading to the recursive forecast structure:
$$\hat{Y}_{t+1} = \alpha Y_{t} + (1-\alpha)\hat{Y}_{t}$$
Through recursive substitution, this shows the exponential decay of past data's influence:
$$\hat{Y}_{t+1} = \alpha \sum_{j=1}^{t-1}(1-\alpha)^j y_{t-j}$$

Selecting $\alpha$¶

Since the choice of $\alpha$ is critical, it is usually selected on a case-by-case basis by simulating values between 0 and 1 to minimize error metrics like MSE or RMSE.

3. Advanced Smoothing Methods¶

Double Exponential (Holt's): Suitable for data with a trend.
Triple Exponential (Holt-Winter's): Suitable for data exhibiting both trend and seasonality.