Skip to content

L18 Diagnostic Checking 1

Normality of Errors

  • How to check if the errors are normal?

    • Check the histogram of the standardized residual, \(\dfrac{\hat{e}_{t}}{\sigma_{e}^{2}}\)
    • Draw normal Q-Q plots
    • Look at Tukey's "five number summary" to check for normality
      • Skewness = 0?
      • Kurtosis = 3?
      • Excess kurtosis = 0?
    • Hypothesis tests
      • Shapiro-Wilk
      • Jarque-Bera

  • If the sample size is relatively small, then the simulated distribution will be skewed even if it is drawn from a normal distribution.

Jarque-Bera Test

  • Tests whether skewness or excess kurtosis are collectively equal to 0 or not?
  • \(\beta_{1}\) = skewness
  • \(\beta_{2}\) = kurtosis
\[ JB = \dfrac{n}{2} \left[ \beta_{1}^{2} + \dfrac{(\hat{\beta}_{2}- 3)^{2}}{4}\right] \sim \chi_{2}^{2} \]

The Hypothesis Setup

\[ \begin{matrix} H_{0} : & \text{Normality} \\ H_{\alpha} : & \text{Non-Normality} \end{matrix} \]

Shapiro Wilk Test

\[ W = \dfrac{\left( \sum_{i=1}^n a_{i}x_{(i)} \right)^{2}}{\sum(x_{i}- \bar{x})^{2}} \]

where,

  • \(a_{i}\) are constants
  • \(x_{(i)}\) denote order statistics.

Reject normality if \(W\) is too small.

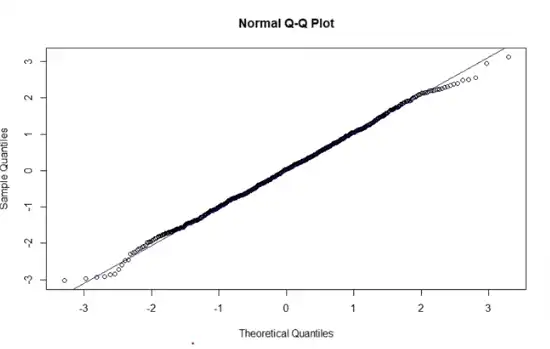
Normal Q-Q Plots

  • 95th quantile (95% of the values are smaller than this 95% quantile)
  • X-axis: Theoretical quantiles (assuming standard normal distribution)
  • Y-axis: Actual quantiles from the sample distribution.

If the graph shows a straight line then normality holds true.

Normality holds:

L18__Diagnostic Checking - 1-1768984649984.webp

Normality doesn't hold:

L18__Diagnostic Checking - 1-1768984671799.webp

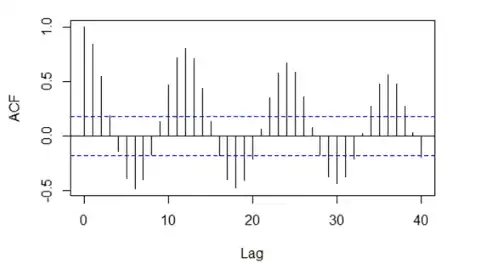
Detection of Serial Correlation

"Serial autocorrelation": Residuals are found to be correlated with their own lagged values.

Draw the ACF plot:

L18__Diagnostic Checking - 1-1768984717059.webp

If there is this kind of pattern in correlations, we can say that there is serial autocorrelation (current error and one error in the future and the past are correlated).

Box-Pierce Test

\[ H_{0}: \text{data are independent (no correlation)} \]

\(h\) is the number of lags up to which we would check for.

$$
Q_{BP} = n \sum_{k=1}^h \hat{\rho}_{k}^{2}
$$
If \(Q_{BP} \gt \chi_{1-\alpha,2}^2\)

  • reject null \(\implies\) Autocorrelation in residuals
  • recheck model → Better add another lag in either AR or MA part of the model.

Ljung-Box Modified Test

  • \(n\) is the sample size, \(h\) is the number of lags being tested
  • Mostly same as #Box-Pierce Test
  • Modified by Ljung and Box in 1978.
    • \(n^{2}\) and \(n-k\) in denominator
\[ Q_{LB} = n^{2} \sum_{k=1}^h \dfrac{\hat{\rho}_{k}^{2}}{n-k} \]