Skip to content

L16 Model Identification

How do we find the best possible model (optimal orders \((p,q)\) of the model) given the practical data?

ACF and PACF plots of AR and MA models

ACF PACF
\(AR(p)\) Tails off after lag \(p\)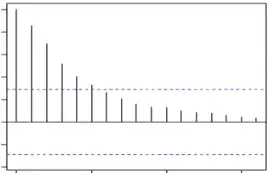

L16__Model Identification-1768981473022.webp		 Cuts off after lag \(p\)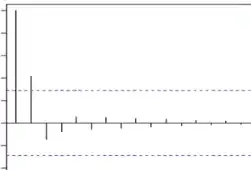

L16__Model Identification-1768981499872.webp
\(MA(q)\) Cuts off after lag \(q\)

L16__Model Identification-1768981499872.webp		 Tails off after lag \(q\)

L16__Model Identification-1768981473022.webp
  • Note the 95% confidence bands, any correlations outside the band are significant.
  • For large and messy data, ACF and PACF become complicated (harder to interpret)
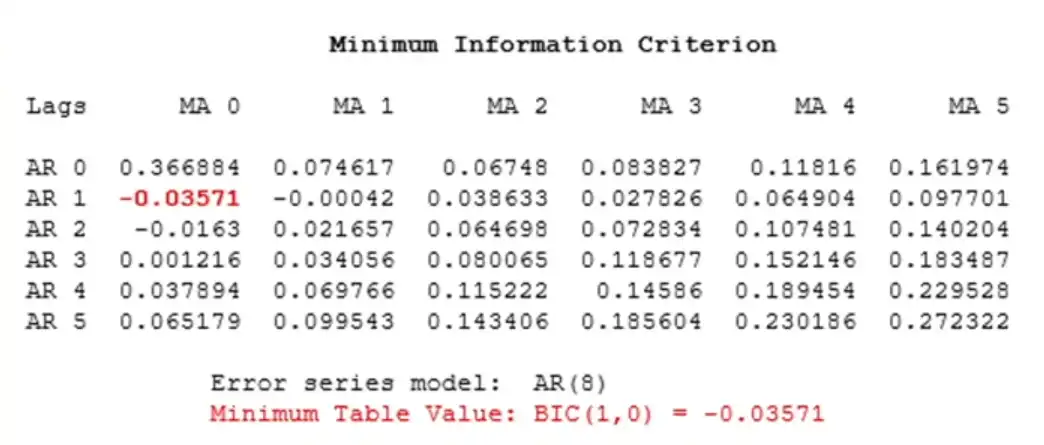
  • There can be multiple models. Choose the most appropriate model (with less parameters) → Look at information criteria.1

Information Criteria

  1. AIC: 1974
  2. SBC (or BIC): 1978
  3. HQIC: 1989

Akaike's Information Criteria (AIC)

A statistical model with \(M\) parameters are fitted to data.

\[ AIC = -2\log(\text{Maximum Likelihood}) + 2M \]

The log-likelihood function becomes

\[ \ln L = -\dfrac{n}{2} \ln 2\pi\sigma_{e}^{2} - \dfrac{1}{2\sigma_{e}^{2}} S(\phi_{p}, \theta_{q}, \mu) \]

where
- \(S(\phi_{p}, \theta_{q},\mu)\) is the RSS,
- assuming \(e_{t}\) follows a \(\mathcal{N}(0, \sigma_{e}^{2})\). \(Y_{t}-\hat{Y_{t}} = e_{t}\)
- The first part \(-\dfrac{n}{2}\ln 2\pi\sigma_{e}^{2}\) comes from the normal PDF

\[ AIC = n \log \hat{\sigma_{e}}^{2} + 2M \]

Schwarz's Bayesian Criteria (SBC) or BIC

A.k.a. Bayesian Information Criteria (BIC)

  • BIC introduces an additional penalty term for an extra parameter, to account for the risk of overfitting that comes with higher number of parameters
\[ SBC = n \log \hat{\sigma_{e}}^{2} + M \log n \]

Hannan-Quinn Information Criteria (HQIC)

\[ HQIC = n \log \hat{\sigma_{e}}^{2} + 2M \log(\log n) \]
  • Due to simplicity people still prefer AIC and SBC.

Other Techniques

  • Sample Inverse Autocorrelation Function (SACF)
    • Generally captures orders better in seasonal models than PACF
    • useful for detecting over-differencing
  • Extended Sample Autocorrelation Function (ESACF)
    • Can tentatively identify orders of stationary or nonstationary ARMA process
    • Based on iterated least squares estimates (previous information criteria were based on MLE)
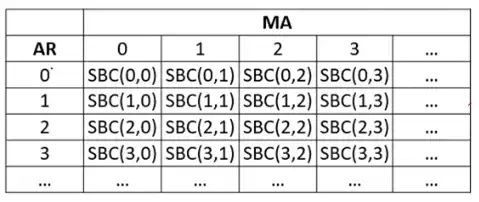
  • Minimum Information Criteria (MINIC)
    • Use a combination of AIC and SBC to minimize overall information
    • L16__Model Identification-1768982729123.webp
    • Which cell gives you the minimum value? Select the orders accordingly.
    • L16__Model Identification-1768982767711.webp

  1. If the same job could be done with approximately same accuracy but less number of parameters, prefer that ↩