Skip to content

Cyclicity and Tests for Stationarity

1. Cyclical Variations

Cyclicality refers to gradual, long-term, and irregular repetitive movements in a time series. Unlike seasonality, these fluctuations do not have a fixed frequency, and the period usually extends beyond a single year.

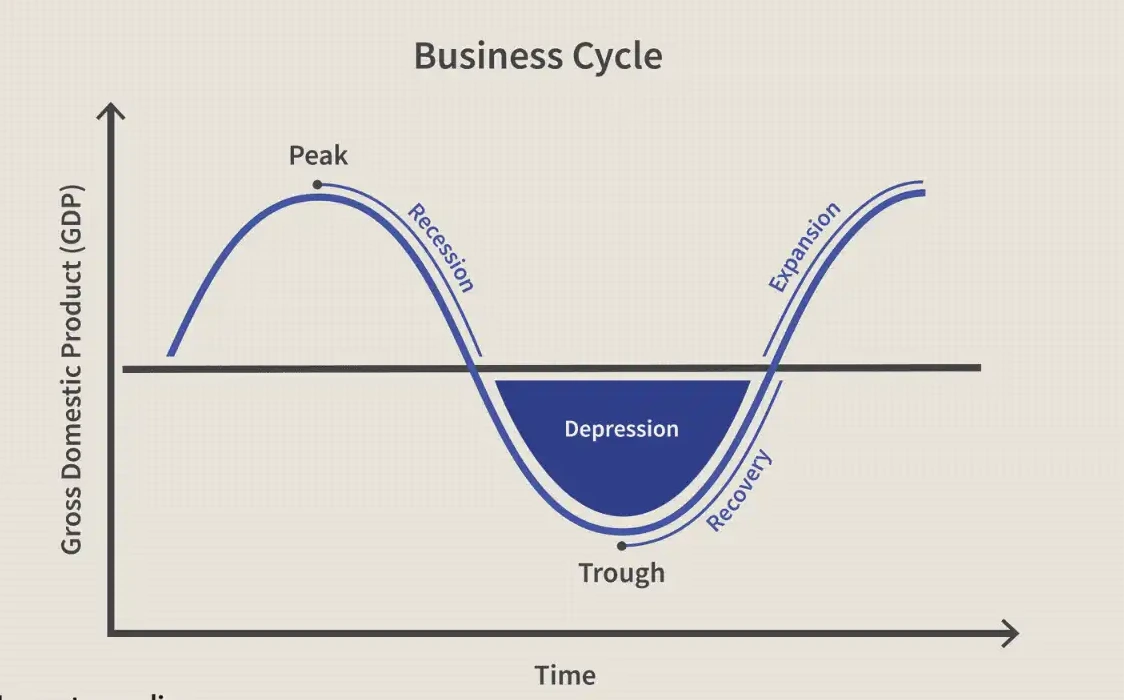
The 6 Phases of a Business Cycle:

  1. Expansion
  2. Peak
  3. Recession
  4. Depression
  5. Trough
  6. Recovery

L13__Cyclicity and Test for Stationarity-1768972967531.webp

Examples:
* Business Cycles: Periodic economic growth and contraction.
* Price Cycles: Influenced by production decisions and supply-demand lags.
* Solar Cycles: Every 11 years, the Sun's magnetic poles shift entirely, impacting solar activity.

2. Seasonality vs. Cyclicality

Feature Seasonality Cyclicality
Origin Calendar Effects Irregular fluctuations
Frequency Fixed frequency No fixed frequency
Length Average length is smaller (\(\le 1\) year) Usually longer than 1 year
Magnitude Generally lower magnitude Magnitude of cycles is higher

3. Unit Roots and Non-Stationarity

A unit root exists when one of the characteristic roots of the model equation is equal to 1.

Unit Root Impact

Unit roots make a process non-stationary because the model will never converge to a constant mean.

Example:
Consider the model: \(Y_{t} - 1.9 Y_{t-1} + 0.9 Y_{t-2} = e_{t} - 0.5 e_{t-1}\).
This can be rewritten using the backshift operator as: \((1 - 1.9B + 0.9B^{2}) Y_{t} = (1 - B)(1 - 0.9B)Y_{t}\).
The roots are \(1\) and \(\frac{10}{9}\). Because of the unit root (\(1\)), the original model is an \(ARIMA(1,1,1)\) and is non-stationary. Once differenced (\(W_t = \nabla Y_t\)), it becomes a stationary \(ARMA(1,1)\).

Why are Unit Roots a problem?
A unit root implies the structure \((1-B)Y_{t} = f(e_{t})\), or \(Y_{t} = Y_{t-1} + f(e_{t})\). This means the current value is simply the past value plus some random error. Consequently, the variance grows over time, and the series does not return to a long-run mean.

4. Tests of Stationarity

Statistical tests help determine if a series is stationary or if transformations are needed.

Augmented Dickey-Fuller (ADF) Test

This test checks for the presence of a unit root.
* \(H_{0}\): Series is non-stationary (Unit root exists).
* \(H_{a}\): Series is stationary.

Kwiatkowski-Phillips-Schmidt-Shin (KPSS) Test

This test checks for a deterministic trend or mean stationarity. Unlike the ADF, the null hypothesis is stationarity.
* \(H_{0}\): Series is stationary.
* \(H_{a}\): Series is non-stationary.

Phillips-Perron (PP) Test

The PP test shares the same goal and hypothesis setup as the ADF test but uses different assumptions about error terms.
* Robustness: It is more robust in the presence of autocorrelation and heteroskedasticity.

Variance Ratio Test

This is a specific test for a random walk.
* \(H_{0}\): Series is non-stationary.
* \(H_{a}\): Series is stationary.
* Logic: If the calculated ratio is significantly different from \(1\), the series is not a random walk.