Skip to content

L12 Seasonality and its Features

  • Note, there is a difference between

    • lag \(d\) difference: \(\nabla_{d} Y_{t}\) and,
    • \(d\)-th difference: \(\nabla^d Y_{t}\)
    • If the trend \(m_{t}\) is a polynomial of order \(d\) then \(\nabla^dY_{t}\) is stationary
    • if the data is seasonal with period \(d\) then \(\nabla_{d}Y_{t}\) will remove seasonality.

  • Seasonality

    • = regular periodic variation where period of cycle \(\leq 1\)
    • usually predictable
    • seasonal factors show repeating behavior
    • Caused by cycle of seasons, holidays, regular changes in behavior, biological rhythms

  • Examples of seasonality

    • Animal migration
    • increase in sales
      • coffee/warm clothes during winter
      • fans/ACs during summer
    • clothes and fire crackers' during Diwali
    • Unemployment in June

  • Reason to study seasonality

    • Better planning for temporal channges
    • Eliminate non-stationarity

Graphical Techniques to detect Seasonality

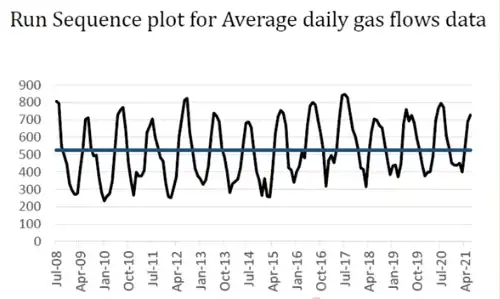
Simple TS or Run Sequence Plot

L12__Seasonality and its Features-1768972165959.webp

  • The mean indicated by horizontal line
  • Quarterly data
  • Identify
    • Seasonality
    • Shift in location (local behavior of drifting away from the mean)
    • Shift in variation

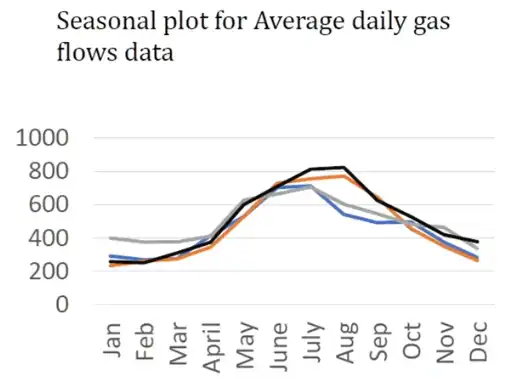
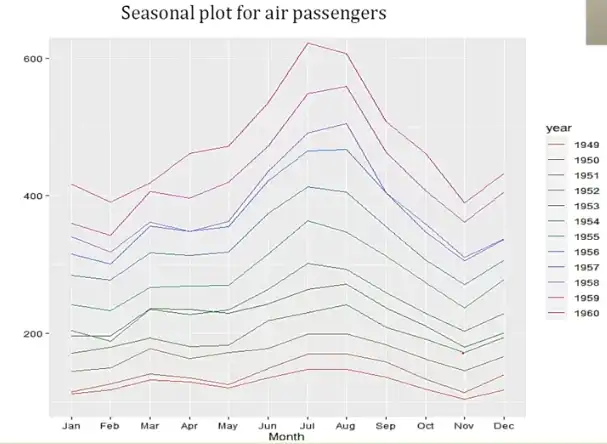
Seasonal Plot

L12__Seasonality and its Features-1768972322813.webp

  • Each color corresponds to one year
  • The graph gives us behavior across years
  • Observe
    • August (2021 (black) > 2023 (blue))

If we observe the Airline Passengers data

L12__Seasonality and its Features-1768972433818.webp

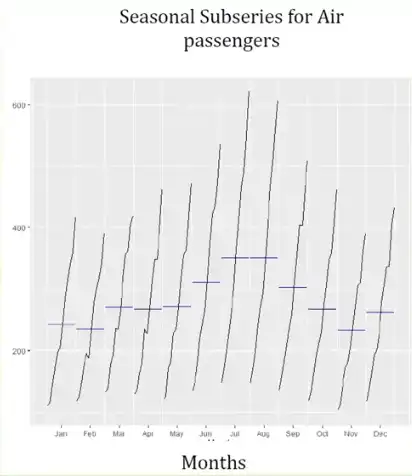
Seasonal Sub-series Plot

L12__Seasonality and its Features-1768972528832.webp

  • Evolution over time is more clearer
    • Extent: From min to max (the range of values)
    • Mean: Blue lines show the mean of the month
  • One can't compare the number between two months

Box-plot

Same as #Seasonal Sub-series Plot but also gives the idea of spread by talking about quartiles.