Greek Letters

Greek letters are the partial derivatives with respect to model parameters that are likely to change.

Risk involved in Option Hedging strategies

Example

• Bank has sold an European call option
  • Price = $300,000
  • # of shares = 100,000
  • Non-dividend paying
• Specs
  • \(S_{0} = 49\)
  • \(K = 50\)
  • \(r = 5\%\)
  • \(\sigma = 20\%\)
  • \(T= 20\text{ weeks}\)
• Black Scholes-Merton value = $240,000

How does the bank hedge its risk to lock in a $60,000 profit?

• Naked position \(\to\) No action²
• Covered position \(\to\) Buy 100,000 shares today¹

But what about the risk associated with these strategies? (Read footnotes)

Thus, we can apply the stop-loss strategy

• Buy 100,000 shares as soon as price reaches $50 (to lock the profit of $300,000, the option premium)
• Sell 100,000 shares as soon as price falls below $50 (as the option call will not be exercised thereafter, and we don't make a loss in the value of the stock)

Black-Scholes-Merton Valuation

The BSM value of the call/put option are related to the various input variables like so:

Input Variable	Symbol	Description	Impact on Option Price
Current Stock Price	\(S\)	The current market price of the underlying asset.	\(\uparrow\) Price \(\implies \uparrow\) Call Value \(\text{ and } \downarrow\) Put Value
Strike Price	\(K\)	The fixed price at which the option holder can buy or sell the asset.	\(\uparrow\) Strike \(\implies \downarrow\) Call Value \(\text{ and } \uparrow\) Put Value
Risk-Free Interest Rate	\(r\)	The theoretical rate of return on a zero-risk investment.	\(\uparrow\) Rate \(\implies \uparrow\) Call Value \(\text{ and } \downarrow\) Put Value
Volatility in stock price	\(\sigma\)	The expected fluctuation or uncertainty of the underlying asset's price.	\(\uparrow\) Volatility \(\implies \uparrow\) Both Call and Put Value
Time to Expiration	\(T\)	The time remaining until the option expires (in years).	\(\uparrow\) Time \(\implies \uparrow\) Both Call and Put Value (generally)

Greek Letters

Definition

Greek letters are the partial derivatives with respect to the model parameters that are liable to change.

• Usually traders use the Black-Scholes-Merton model when calculating partial derivatives
• Practitioner Black-Scholes model: \(\sigma\) in BSM is set = implied volatility when Greek letters are calculated.

NOTE: We will denote option price, \(P\) for put, \(C\) for call and \(\Pi\) for both in general.

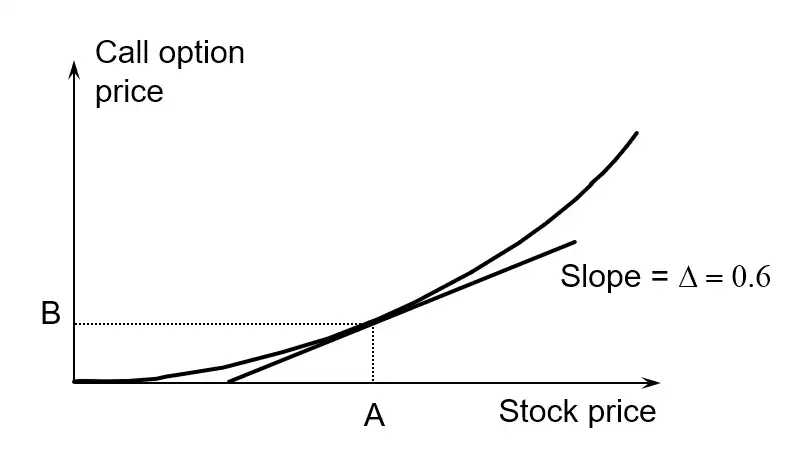
Delta \(\Delta\)

Definition

Delta is the rate of change of the option price with respect to the underlying asset price

\[ \Delta = \dfrac{\partial \text{Option Price}}{\partial \text{Underlying Asset Price}} = \dfrac{\partial{\Pi}}{\partial{S}} \]

• Here the \(\Delta =0.6\)

Example

• Stock price, \(S_{0} = 100\)
• Call option price, \(C = 10\)³
• Investor sold call option to buy 2000 shares
• Hedge by buying \(\Delta \times 2000 = 0.6 \times 2000 = 1200\) shares

  Gain(loss) on stock position \(\overset{\text{Offset}}{\iff}\) Loss(gain) on option position

• If stock price rises by $1
  • Gain is $1200 (in stock position)
  • Loss is $1200 (\(= 0.6 \times \$1 = \$0.6\), in options position)
• We did this buy noting
  • \(\text{change in }C= \Delta \times\text{change in }S\)
  • \(\Delta_{C} = \dfrac{\partial{C}}{\partial{S}}\), \(0 \leq \Delta_{C}\leq1\)
  • \(\Delta_{P} = \dfrac{\partial{P}}{\partial{S}}\), \(-1 \leq \Delta_{P} \leq 0\)

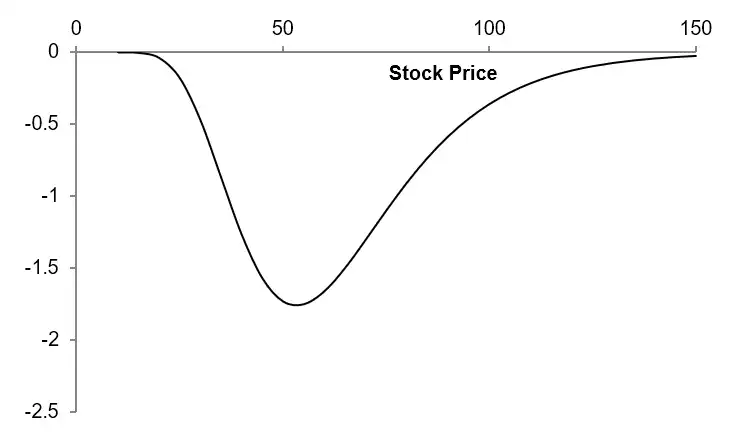
Theta \(\Theta\)

Definition

Theta of a derivative (or portfolio) is the rate of change of value with respect to the passage of time (i.e. time to maturity) with ceteris paribus.

\[ \Theta = \dfrac{\partial\text{Value of Portfolio}}{\partial{\text{Time to Maturity}}} = \dfrac{\partial{f}}{\partial T} \]

\(\Theta_{C}\), Theta for call option
with \(K=50, \sigma=25\%, r=0, T=2\).

• The \(\Theta\) of a call or put is usually negative.
  • The value, (\(P\) or \(S\)) of a long⁴ call or put option, declines when \(T\) increases, if the price of underlying, \(S\) and volatility, \(\sigma\) remain the same.
• Change in option value, \(P\) or \(S\) = \(\Theta \times dt\)
  • where \(dt = \dfrac{1}{252}\text{years} \sim 0.004\text{ years}\) (one trading day)
  • If \(\Theta_{C}=-13.5\) then after one day, change in \(C = -13.5 \times 0.004 = -0.054\)

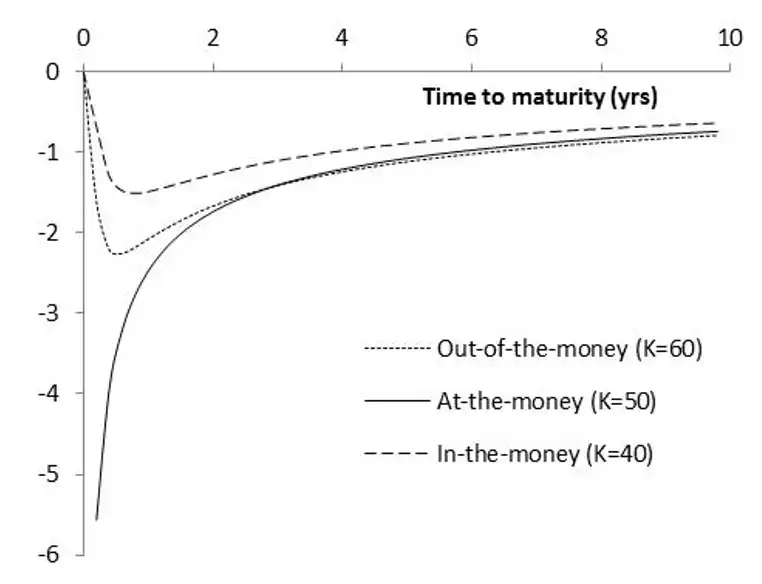
Variation of \(\Theta\) with various strikes, \(K\)

Variation of \(\Theta\) with Time to Maturity for various \(K\)
and \(S_{0}=50, r=0, \sigma=25\%\).

• \(\Theta\) is less negative for option that are close to the money

Gamma \(\Gamma\)

Definition

Gamma is the rate of change of delta with respect to the price of the underlying.

\[ \Gamma = \dfrac{\partial{\Delta}}{\partial{\text{Price of Underlying}}} = \dfrac{\partial^{2}{\Pi}}{\partial S^{2}} \]

• \(\Gamma\) is greatest for options that are close to the money.

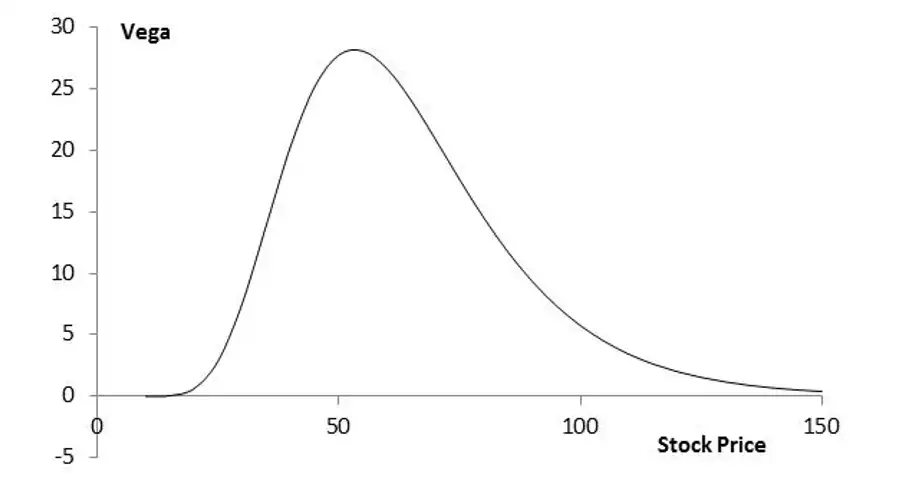
Vega \(\mathcal{V}\)

Definition

Vega is the rate of change of value of a derivatives portfolio with respect to volatility

\[ \mathcal{V} = \dfrac{\partial{\text{Value of Portfolio}}}{\partial\sigma} = \dfrac{\partial{f}}{\partial{\sigma}} \]

• If \(\mathcal{V} = 12.1\), it means
  • At 1% increase in implied volatility⁵, \(\sigma\) the increase in value of the option \(=0.01 \times 13.1 = 0.121\)

Vega, \(\mathcal{V}\) for call or put option
(\(K=50, \sigma=25\%, r=0, T=2\))

Rho \(\rho\)

Definition

Rate of change of value of a derivative with respect to the interest rate with ceteris paribus.

\[ \rho = \dfrac{\partial{\text{Value of Derivative}}}{\partial{\text{Interest Rate}}} = \dfrac{\partial{f}}{\partial{r}} \]

• If \(\rho=8.91\) it means
  • a 1% increase in the risk free rate, increases the option value by \(0.01\times 8.91=0.0891\)

Why need Greeks?

• Greeks contain information about option sensitivity into something that can be visualized.
• Magnitude of changes can be compared and used to offset each other.
• Can easily be extended to an entire portfolio on a given underlying.

---

1. If stock price declines to $40, buyer will not exercise call option. Thus, we just experience loss on shares as $900,000, while the price of option was $300,000. ↩

2. Say we don't have the shares. If the price rises to $60, we have to buy the shares at that spot price and sell it to the buyer of the call at $50, thus incurring a total loss of $1,000,000, while the price of option was $300,000. ↩

3. In case of put option, we write \(P\) ↩

4. Note that long position refers to the act of buying or holding the option (not the underlying or what-so-ever) ↩

5. For implied volatility refer to Practitioner Black-Scholes ↩