Lecture 56 Problems with Classical Game Theory III
Cognitive Processes & Strategic Reasoning¶
- CGT doesn't explicitly model cognitive process (underlying choices), though studies have shown that it would help to do so.
- 2002 study: Three-round Rubinstein bargaining game
- Can be solved through backward induction
- But most people solved it using first round data (forward induction)
- Backward-looking logic is not natural to people
Thus,
- Cognitive cost is non-trivial
- Deviations not from irrationality but complexity of the process
Failures in Signaling Games¶
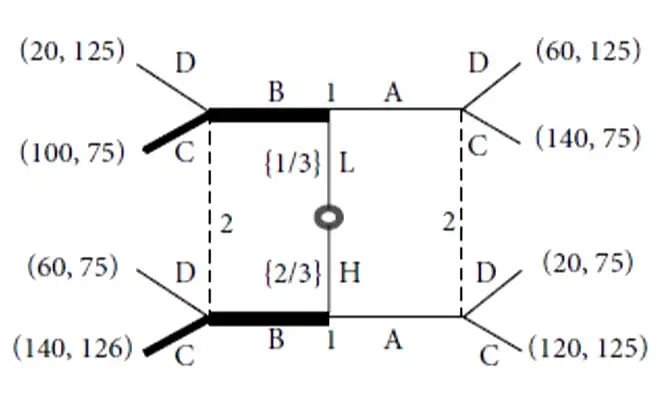
- Signaling games \(\to\) substantial cognitive demands on players
Sender (P1) and Receiver (P2)
- Nature moves first (oval circle)
- Who's going to pay? Randomly chosen
- H: 2/3
- L: 1/3
- Who's going to pay? Randomly chosen
- Who plays is revealed to P1 (not to P2… P2 doesn't know if it is H or L)
- H or L, i.e. P1 can play
- A
- B
- Even if P1 plays A or B, P2 doesn't know if it is "H ka A" or "L ka A" (that's why the dashed line)
- Two Intuitive equilibria here: shown by bold lines.
Intuitive equilibria were played… as more number of rounds were played. "Unintuitive" equilibria were not played.
- Separating equilibrium = each agent's first period strategy is a 1-1 of his type (i.e. H or L) so first-period action reveals his type.
- Thus, agents are playing a game of complete information
- Semi-pooling = at least one of the first-period strategy is not 1-1
- Completely Pooling = constant functions…
Previous game outcome has Pooling equilibrium
- Gradually, players starts to shift towards pooling behavior (constant instead of updating using prior beliefs)
Correlated Equilibrium = joint payoffs \(\gt\) highest payoffs from any NE.
- (D,L) and (U,R) are NE
- MSE = \(P(U) = 0.6\), \(P(L)=0.6\)
- Say, payoff = utility
Recommended strategy are NE, if they don't play it (self-enforcing). This implies that
- Monetary payoff \(\neq\) Utility
- Players may have social preferences
- Players may doubt rationality of other players
So, which of these two or both hold?
Compliance was higher with robotic agents… but not with human (don't have trust in rationality of other individuals)
"Subjects don't switch because they believe that their opponents also won't switch"
- Players need assurance about compliance
Strategic Complements, Substitutes & Nominal Rigidity¶
- Monopolistically competitive environment where payoff \(= f(\text{their price},\text{Inflation},\text{Nominal Money Supply})\)
-
Two behavioral factors
- Money illusion
- Anchoring
-
The extent of BB is endogenous, depends on whether strategic interaction is SC or SS
- Less costly (forgone payments) \(\implies\) BB less likely
Competitive Equilibrium: Experimental Limitations¶
- CE = all consumers and firms act optimally and markets clear
- these models depend on strong assumptions e.g. no trade at non-equilibrium prices
- Presence of Walrasian auctioneer (fiction) = he sets the equilibrium prices based on the truthfully reported intended trades in all markets at that price
- Mechanics
- Initial price (CE) price vector = \(p^*\)
- Excess demand \(\gt 0\) \(\implies\) auctioneer increases the price in those markets.
- Finds the price where excess demand = 0.
- Global uniqueness of \(p^*\) \(\impliedby\) All goods be gross substitutes at all prices
- Need (infinite) large number of atomistic (small) buyers and sellers, none of each should be large enough to influence actual market outcomes.
- All are price takers.
Classical model: buyer, sellers and auctioneer have full information
-
None of the participants can influence the market in a strategic manner (they will take the price)
-
Assume no market frictions, imperfections, externalities and no public goods.