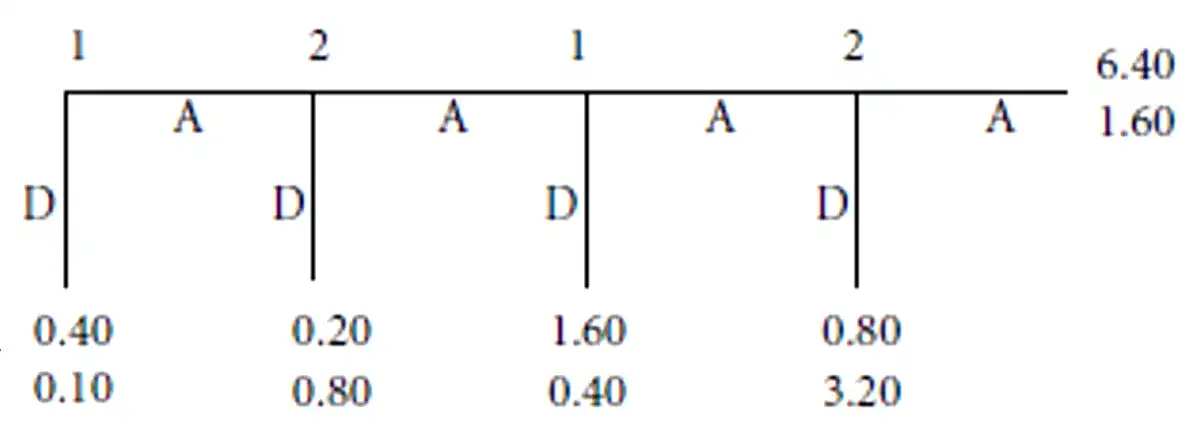
Lecture 55 Centipede Games

• Rosenthal 1981
• Specs
  • Two players, alternating moves
  • D, A and pass
  • Payoff at terminal node
  • At each move, take 80% of growing pie and end of the game
  • or 'pass' with the pie doubling with each move.

• Unique NE: P1 plays D at the very first game…
• This is a pareto inefficient outcome to choose A at the final node.

Experiments show:
1. Very little evidence of D outcome (Backward induction)
2. \(P(\text{playing D})\) increases as we move closer towards the last node.
3. Evidence appears to be mixed.

Mixed Strategy Nash Equilibrium (MSE): Empirical Failures

Empirical validity of MSE has been questioned.
- Players often deviate from MSE predictions
- Shachat (2002)… people play mixed strategies but mixtures are significantly different.
- Randomization behavior != Classical theory
- Strengthened the case for alternative models (w/ bounded rationality)

Mookerjee & Sopher rejected MSE at individual and aggregate levels.
- Persistent failure of players to converge with MSE on repeated rounds
- Decisions influence with external factors \(\implies\)behaviorally grounded theories required.

Collins & Sherstyuk studied three-firm Hoteling competition model.

Rapoport & Amaldoss investigated R&D investment game with unique MSE

Aggregate level conformity to MSE to some extent. Individuals completely deviated.

Coordination Failures

• Imperfect competition macroeconomic models
• Network externalities and standards
  • IT or process or standard is commercially viable if a critical number of users coordinate on adopting it
• Pure strategy payoffs give (200,600) or (600,200). The mixed strategy expected payoff gives 150 per player, which is worse than coordinating on any of the two NEs.
• Empirically, pure strategy NE was played < 42% of the time.
• Widespread coordination failures

Multiple Equilibria

• CGT assumes players will coordinate on an equilibrium… but limited guidance on which equilibrium will emerge.
• Coordination failures \(\implies\) Question predictive power of CGT

Classification of coordination games
- Payoff-Symmetric: Shelling's classic meeting game (relies on focal points for coordination)
- Payoff-Asymmetric: BoS (pre-play communication and timing can influence outcomes)

Median Action Games = Players' payoffs depend on action and the group's median action
- Players failed to converge
- Payoff/Risk dominance couldn't account for observed behavior
- History-dependent (early-round outcomes influenced)
- In absence of communication, players use salient or focal points.

Focal point: Players tend to choose those strategies whose labels are salient. Equilibrium resulting from such choices = focal point.

• Primary salience = actions that are salient for a player
• Secondary salience = coordinating on actions that are believed to have primary salience for other players.

Test for these concepts

• Two groups
  • C: Coordinating condition (payoff depends on action of others)
  • P: Picking condition (payoff independent of any coordination)
• Group C was relatively more successful at coordinating actions.
  • \(c:\) coordination index, a measure of probability that individuals chosen at random will coordinate on their actions
    • Distinct choices, \(c=0\)
    • Identical choices, \(c=1\)
    • Between the two extremes, partial coordination

Labels convey important information that can help coordinate actions.

• Despite high degree of salience, \(c \lt 60\%\) for the first 10 questions for group C.

---

There are several factors that influence coordination outcomes, none of which are adequately captured by CGT.
- Outside options and forward induction influences predicted outcomes.
- Framing effects
- Timing of moves
- Pre-play communication

Forward Induction, Timing

• Example of BoS with an addition
  • Two phases
  • Phase I: P1 can choose between \(X\) and BoS game… where \(X \in(200,600)\)
  • Phase 2: BoS game

\[ \begin{matrix} & \text{Theatre} & \text{Concert} \\ \text{Concert} & (0,0) & (200,600) \\ \text{Theatre} & (600,200) & (0,0) \end{matrix} \]

• P2 will use forward induction. "If P1 has decided to forgo (200,600) then he is definitely after (600,200)", so he will choose Theatre…

  • Thus P2 will coordinate expectations and play "Theatre".

• But if \(X = 100\), then nothing can be inferred about P1's intentions.

Outside options, framing effects (normal/extensive form) and timing issues influence the level of coordination.