Skip to content

Lecture 54 Problems with Classical Game Theory I

The Challenge of Testing Classical GT

  • Empirical findings: systematic deviations between theoretical expectations and actual human behavior. Assumptions don't hold in practice:

    • rationality
    • strategic reasoning
    • equilibrium selection

  • Why test? To understand how real people behave in strategic situations (vs Econs)

    • bounded rationality
    • social preferences
    • framing effects
    • assurance
    • resentment
    • reciprocity

Enter Behavioral Game Theory.

Classical prediction Empirical evidence
Players solve by iteratively deleting dominant strategies Able to engage only a few steps of iterative dominance (higher is rare)
Assume that players and the belief that opponents are rational Are they?

Suppose \(j\) steps of iterated deletion of dominated strategies.
- \(j=1\), predictions of GT hold
- \(j=2\), majority violate
- Possibility: people have lesser confidence in the rationality of others to engage in IDDS. But there's two problems:
1. If P1 is rational, why does he believe P2 is not?
2. If P2 is believed to be irrational in simple games, then paapam (hardly any games exist where notion of rationality comes)

Suppose a game, 100 people pick a number between 0 to 100. The average of the numbers will be taken, the person with the number closest to 2/3 of the average will be considered winner.
- If everyone picks 100, then the winning number would be 67, no rational player would pick more than 67… but then everyone is rational
- So everyone picks 67… 44…33… all the way down to zero
- NE is zero (0).

But players chose 22 to 33… as they assumed others will not iterate more than 2-3 steps… or didn't play NE strategy even if they know it.

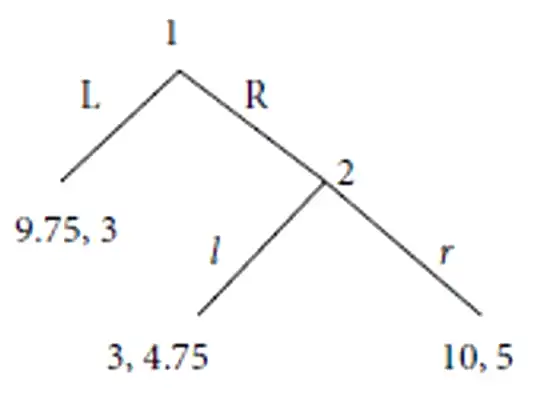
Failure of Two Steps of Iterated Dominance

assets/images/2025/11/Lecture%2054__Problems%20with%20Classical%20Game%20Theory%20-%20I-1761970970071.webp

  • P1 lacks confidence in the rationality of the opponent and thus would select the \(L\) even though (R,r) would be the NE strategy.
  • \(p= 0.97\) (that P2 will play \(r\) if P1 played \(R\))
  • But experiment showed \(q = 0.83 \lt 0.97\)
  • Thus, the P1 (66%) cannot be called irrational.

There are doubts about mutual rationality.

A Dynamic Game of Perfect Information

  • P1 proposes a split of $5.
  • If accepted by P2, game ends
  • If rejected… the pie size shrinks to $2.
  • P2 proposes a split of $2
  • If accepted by P1, game ends

  • If rejected… no one gets anything.

  • NE split:

    • P1 keeps $3, and P2 gets $2
  • Experiments showed:
    • P2 kept $2.83 (close to $3) and P2 got $2.17 (thus they accept it)
  • But when pie shrank from $5 to $0.5
    • P2 kept $3.38 (much lower than $4.5)
    • not rational!

Framing Effects

  • Normal form: 43\% chose R while extensive form 92\% chose R

Extensive form are frames which makes the dominant strategies more explicit

  • Cognitively easier for players to spot dominated strategies.
  • Visual structure illustrates sequential moves.
  • Only 16% of P1 and 26% of PE chose equilibrium sequence with 3-steps reasons.
  • Most player chose the safest (avoiding more steps)
  • Games presented through verbal descriptions also altered player's ability to reason through.

Problems

  • Players may possess "other-regarding preferences" (relative payoff instead of absolute payoff)
    • P2 reject offers perceived as unfair even at a personal cost