Lecture 53 Sequential Game & Types of Games
Sequential Nash Equilibrium¶
- Sequential = Games with multiple stages
- Use tree-like representation… extensive form
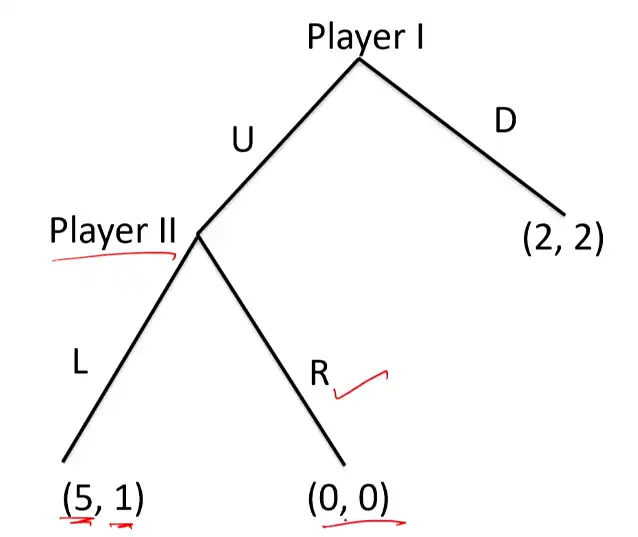
E.g.
- Two stages
- Stage one,
- Player I plays U or D
- Plays D
- Both players get payoff of 2
- Plays U
- Player II's turn
- Stage two,
- Player II plays L or R
- Plays L
- I gets 5
- II gets 1
- Plays R
- Both get 0
- What is NE here?
Subgame-Perfect NE¶
- Subgame of a game = a part of a game, which itself constitutes a game
- Subgame-perfect NE \(\implies\) strategy profile that has NE in each subgame
To find out if it is subgame-perfect… start at the end and use backward induction.
The only subgame perfect Ne is \((U,L)\)
In the entire game, if written as a normal form
\[
\begin{matrix}
& \text{L} & \text{R} \\
\text{U} & (5,1) & (0,0) \\
\text{D} & (2,2) & (2,2)
\end{matrix}
\]
- P1 = U,
- P2 = L
- P1 = D
- P2 is indifferent between L and R
- P2 = L
- P1 = U
- P2 = R
- P2 = D
So the two NE's are \((5,1)\) and \((2,2)\).
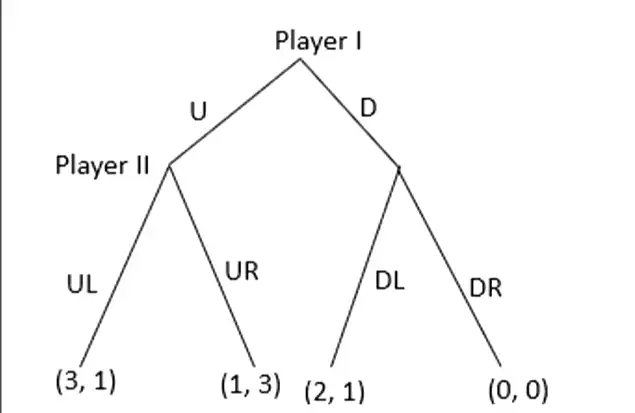
Example¶
- Start with backward induction…
- For P1 (since he makes the first choice)
- UR if U, util = 1
- DL if D, util = 2
- Better of at D so SPNE is \((D,DL)\)
For the normal form representation
\[
\begin{matrix}
& \text{L} & \text{R} \\
\text{U} & (3,1) & (1,3) \\
\text{D} & (2,1) & (0,0)
\end{matrix}
\]
- select U \(\to\) select R \(\implies\) (U,R) is NE
- select D \(\to\) select L \(\to\) select U \(\to\) select R \(\implies\) (U,R) is NE
Normal NE is different from SPNE
Types of Game¶
1. Cooperative & Non-cooperative¶
- Can communicate and collude
- Enter into third-party enforceable binding contracts (prohibited by law)
- Most of economic situations: non-cooperative
- Self-enforcing reliance relationships
- Many games involve mix of cooperation and competition (Prisoners' Dilemma)
2. Two-Player & Multiplayer Games¶
- Can be extended to more than two parties
- More than two players increase the change of defection (one-shot game)
- 'the tragedy of the commons' = property rights are untradeable, unassigned (pollution)
- Important to defect before others do
- can be prevented only if they can be detected and punished
- e.g. Depletion of fish stocks in North Sea
- Undersupplied resources (public goods) instead of being overused
- Opportunity to form coalitions against others (which would otherwise be unsustainable) \(\to\) cartels (oligopoly)
3. Zero Sum & Non-zero Sum Games¶
- a.k.a. Constant sum games
- Gain of one is the loss of another
- Applies in derivative markets (between two speculators)
- Even if gains and losses (monetary) offset… but the utilities may not because of loss-aversion \(u(-100) > u(100)\)
4. Complete & Incomplete Information Game¶
- In practice, players are uncertain about payoffs of each pair of strategy
- either their own payoff
- of that of others
- e.g. Insurance companies may not know all relevant details \(\implies\) adverse selection (Information asymmetry)
- Before transaction: adverse selection (trading partner not giving us the optimal result)1
- After: moral hazard (both the company and myself land into trouble)
- Bidders at auction will not know valuations that other parties place
5. Static & Dynamic Games¶
- Static: Players make their move simultaneously (without knowing move of other players)2
- Dynamic: (IRL) One moves first, other moves afterwards knowing the move of the first.
- e.g. The Ultimatum bargaining game: One proposes a split 50-50 and the responder has to accept or reject it.
6. Discrete & Continuous Strategies¶
- Discrete = Each action is chosen from a limited number of alternatives
- e.g. PD: to confess or not
- Continuous = Limitless alternatives
- e.g. Oligopoly: virtually limitless number of prices
- \(\implies\) Analytical approach is different in terms of mathematical techniques involved.
7. 'One-shot' and Repeated Games¶
- Short-run decision in business (pricing & ads) \(\to\) Repeated games, continuous interaction between competitors, changing their decisions at regular intervals
- Some games may have finite number of rounds
- Some may seem infinite or open-ended
- Long-run decisions (investment) \(\to\) 'one-shot' . The time interval between decisions is several years.
- The next decision scenario involves different payoffs
Summarizing Analytical Game Theory¶
- Descriptive interpretation: GT captures the (actual) manner in which people behave and engage in strategic interactions
- GT \(\implies\) players jointly choose equilibrium strategy profile
- Depends on the equilibrium concept too
- Normative interpretation: GT describes how rational people behave when they engage in strategic interaction
- GT \(\implies\) same as above (2 points)
GT demands are very hard to meet. e.g. Employing backwards induction requires us to think ahead all way to the last round and work back to the present moment.
- Nature of the game is defined by utility distribution in the matrix
- Without known this distribution, we don't won't know the game
- If we don't know the game, we cannot use the GT tools to analyze the interaction.
- A game need not have a unique equilibrium
- Analytical GT doesn't tell us anything about what the equilibrium is or what should be played. :( \(\implies\) Theory is indeterminate
- Some games have infinite number of equilibria \(\implies\) Radically indeterminate
Thus, we need to augment with additional theory to determine predictions
- e.g. Theory of Focal points (2005 Nobel Laureate Thomas C. Schelling)
- Some equilibria stand out in the minds of players…
- and they will frequently select such equilibria
- But the precise feature is far from obvious