Lecture 49 Naive Quasi Hyperbolic Discounting

An Example

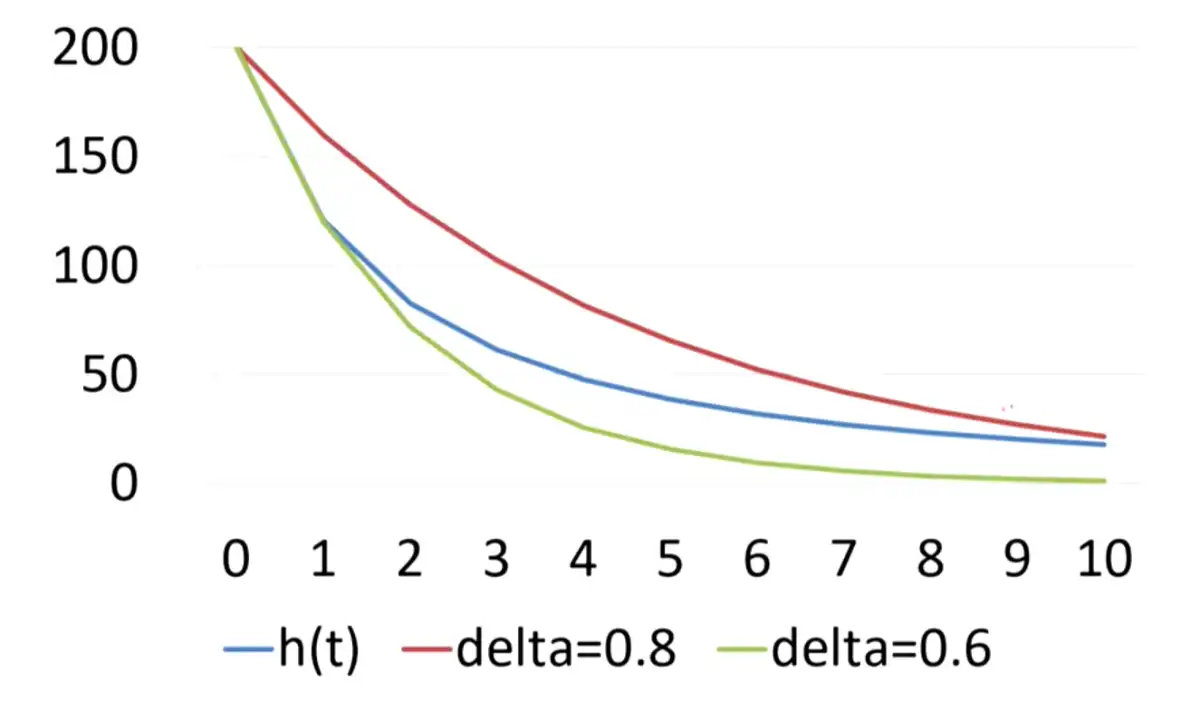
\[ \begin{array}{|c|c|c|c|c|c|c|} \hline t & h(t) & U(h) & \delta(1)=0.8 & U(e1) & \delta(2)=0.6 & U(e2) \\ \hline 0 & 1 & 200 & 1 & 200 & 1 & 200 \\ \hline 1 & 0.603682 & 120.7363 & 0.8 & 160 & 0.6 & 120 \\ \hline 2 & 0.414087 & 82.81733 & 0.64 & 128 & 0.36 & 72 \\ \hline 3 & 0.306454 & 61.2909 & 0.512 & 102.4 & 0.216 & 43.2 \\ \hline 4 & 0.238528 & 47.70567 & 0.4096 & 81.92 & 0.1296 & 25.92 \\ \hline 5 & 0.19245 & 38.49002 & 0.32768 & 65.536 & 0.07776 & 15.552 \\ \hline 6 & 0.159508 & 31.90154 & 0.262144 & 52.4288 & 0.046656 & 9.3312 \\ \hline 7 & 0.134997 & 26.99943 & 0.209715 & 41.94304 & 0.027994 & 5.59872 \\ \hline 8 & 0.116179 & 23.23572 & 0.167772 & 33.55443 & 0.016796 & 3.359232 \\ \hline 9 & 0.101359 & 20.27184 & 0.134218 & 26.84355 & 0.010078 & 2.015539 \\ \hline 10 & 0.089443 & 17.88854 & 0.107374 & 21.47484 & 0.006047 & 1.209324 \\ \hline \end{array} \]

Quasi-Hyperbolic Discounting

• Proposed by David Laibson
• Since the hyperbolic discounting is mathematically difficult
• QH is an approximation
• Separates into two different factors (second period and each additional period)

\[ u(C_{0}) + \sum_{i=1}^T \beta \delta^i u(C_{i}) \]

Consumption in the future receives some penalty. Trading off consumption between two different periods in the future, doesn't face a steep penalty.

• \(0 \lt \beta \lt \delta \lt 1\). \(T \to \infty\)
• \(\beta:\) Second period discount factor
• \(\delta:\) For subsequent periods

Advantages
- The mathematical form resembles ED (simple) but the shape is QH
- We can obtain a closed form solution for consumption of all other periods. (can't do so for HD)

Discounts for longer periods are much smoother \(\implies\) Hyperbolic nature of discounting

Hyperbolic discounting calculation example

• On Friday: we will choose not to eat the cake, as it gives us lower utility
• On Saturday however, will will choose to eat the cake! Time inconsistent behavior.