Lecture 48 Naive Hyperbolic Discounting

SNAP Example

• Supplemental Nutrition Assistant Program
• Debit card for food.
• 50 mil Americans
• $75 billion per year cost

If instead of the SNAP budget, \(s\) the recipient were given a smaller cash transfer (which won't be binding), they would be better off \(\implies\) the policy is inefficient.

• Also, rising number of SNAP participants who are overweight or obese.
• Study: those with SNAP benefits consumed 100 or 200 more calories than those receiving cash.
• Finding of another study:
  • Spending on food in the first two days after receiving food stamp increases by about $5 per person per day.
  • Per day around $2
  • Daily calories consumed per day drops by 10% in the last week.
  • \(c_{j}\) should be relatively close to \(c_{k}\) if \(j\) and \(k\) are close \(\implies\) consumption smoothing
• Rational model: recipients will have foresight to conserve their money and consume a level annuity of food.

But that doesn't happen! Does it?

Naive Hyperbolic Discounting

• A model of time inconsistent preferences

• Discounting varies by time horizon

• Hyperbolic discounting replaces \(\delta^t\) with \(h(t) = (1+\alpha t)^{-(\beta/\alpha)}\)

• And thus maximize \(U = \sum_{i=1}^T h(t)u(c_{i})\)

• Question

  • 1 apple today, 2 tomorrow?
  • 1 apple (1 year) from now, 2 (one year + 1 day) from now
  • Violation of stationarity property
• Daily discounting factor:

\[ \Psi(t,t+1) = \left(\dfrac{1+\alpha(t+1)}{1+\alpha t}\right)^{-(\beta/\alpha)} \]

converges \(\to\) \(1\) as \(t\) gets large.

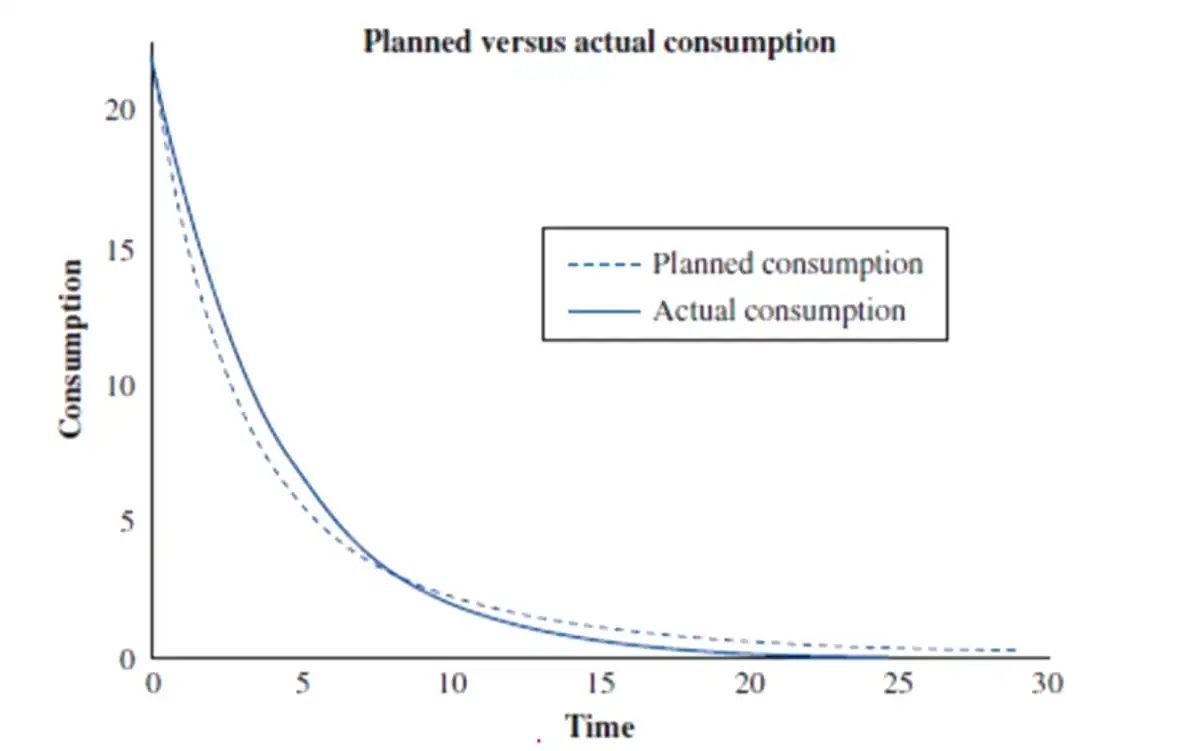
SNAP recipient who behaves according to hyperbolic discounting: Consume a lot today… hope to smooth out her consumption for the rest of the month.

But since she is time inconsistent, she doesn't live by her plan and consumes more today and hopes to smoothen out for tomorrow, every single day in the future.

\[ \hat{\Psi}(1,2) = \Psi(0,1) \]

They put off consumption smoothing until a later date… continue to do so until they reach a point where they no longer have enough food to last the rest of the month.