Lecture 43 Projection Bias
College Admission¶
- Interesting observation, Uri Simonson: Visiting on bad weather days increases the probability that the potential student will actually enroll.
- Visiting when there is significant cloud cover can make outdoor activities less attractive…
- People evaluate the options they will face in the future with a bias by the options currently at hand.
Making Decisions for Our Future Self - Projection Bias¶
- both College Admissions and Kidney Disease scenarios deal with projection bias
People believe they will value options in the future the way they value them today \(\implies\) Projection bias (but time changes, doesn't it?)
- At university, student choose to engage in activity to obtain
- utility: \(u(\text{activity}|\text{university},w)\)
- activity \(\in \{ \text{study},\text{recreate} \}\)
- university \(\in \{ \text{prestige}, \text{party} \}\)
- \(w \in \{ \text{cloudy},\text{sunny} \}\)
If \(u(\text{study}|\text{prestige},\text{cloudy}) - u(\text{study}|\text{party},\text{cloudy})\) is smaller than \(u(\text{recreate}|\text{party},\text{sunny})- u(\text{recreate}|\text{prestige},\text{sunny})\) then overall
regardless of the weather on the day of visit, and vice-versa if the inequalities are reversed.
But if the future utility is gauged based on present conditions such that
and
Thus they would be led to choose the prestigious university (the \(N\) instead of giving equal \(\dfrac{N}{2}\) weights to both types of days, comes from the projection bias).
They will regret it in the future (if they are subject to this projection bias.)
"Aray bro maine socha tha kuchh… but kya se kya hogaya dekhte dekhte…"
-
Time Inconsistent preferences, when people think they will have one set of preferences in the future, but end up with inconsistent preferences.
-
They don't realize how much better off they would be (the difference/gap) at the party school on sunny days.
Person receives utility \(u(c,s)\) from consuming bundle \(c\) at state \(s\) (external conditions).
- Suppose someone is in state \(s'\)
- He needs to predict \(u(c,s)\). His predicted utility \(\tilde{u}(c,s|s')\)
- His bias is (with \(0 \leq\alpha \leq 1\))
-
\[ \tilde{u}(c,s|s') = (1-\alpha)u(c,s) + \alpha u(c,s') \]
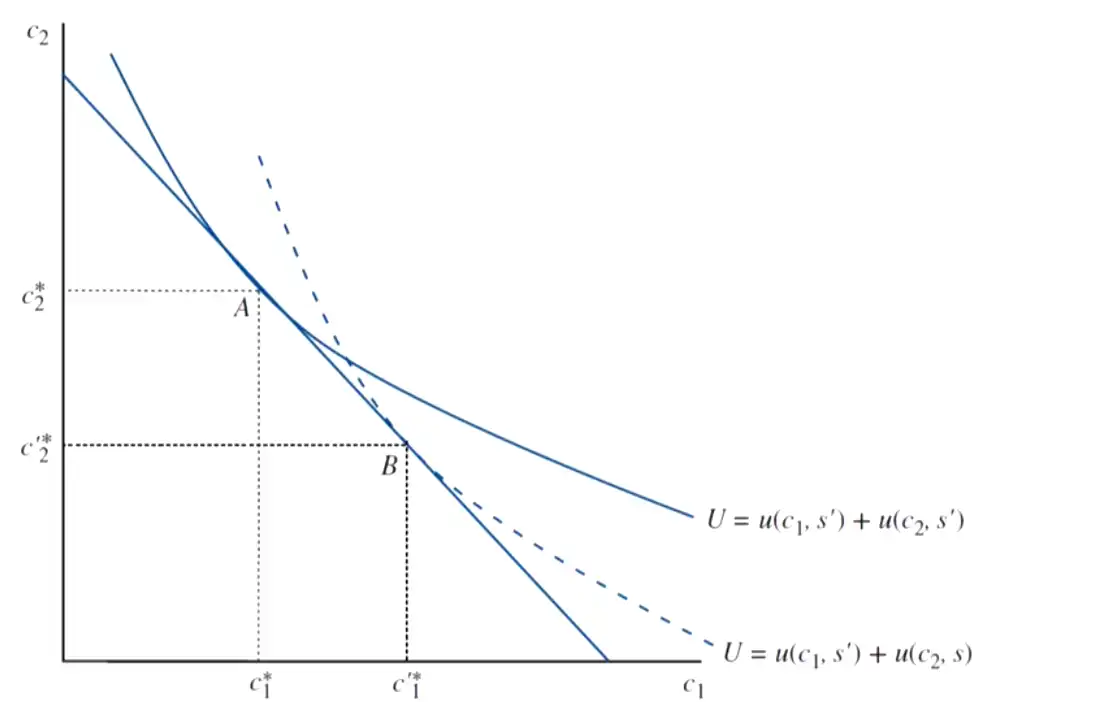 Notice the bias that leads to outcome \(B\).
Notice the bias that leads to outcome \(B\).
- \(\alpha=1\) \(\to\) \(A\) (closer to the origin, worse off)
- and anywhere in between
- \(\alpha=0\) \(\to\) \(B\)
*[DUM]: Discounted Utility Model