Lecture 42 Optimal Consumption in the Two Period Model

The budget constraint with equality can be written as…

\[ C_{1} = A - (1+r)C_{0} \]

called the intertemporal budget line.

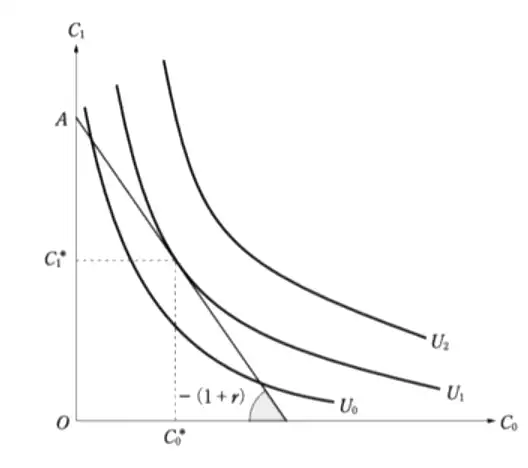
Let $U_{i}$ be a level of utility (constant), then the collection of ($C_{0},C_{1}$) such that $U(C_{0},C_{1}) =U_{i}$ is called the IC.

In economics, because $U_{0} \lt U_{1} \lt U_{2}$, the shape of IC is convex toward the origin.

$(C_{0}^*,C_{1}^*)$ is the combo that maximized utility under budget constraint
If $C_{0}^* \lt Y_{0}$, consumer saves the difference
If $C_{0}^* \gt Y_{0}$, consumer borrows the difference
IC of a patient consumer = gradual

When present consumption, $C_{0}$ increases by 1 unit, $C_{1}$ needs to decrease by a relatively small amount to keep the same utility.

…$C_{1}$ needs to decrease by a relatively large amount…

Impatient also saves less and borrows more. Thus, slope is important for savings and borrowing decisions.

Slope of IC is negative, and its absolute value = MRS
$$
=\dfrac{\text{Marginal Utility of Present consumption}}{\text{That of future consumption}}
$$

Thus, MRS = $\dfrac{\partial U(C_{0},C_{1})/\partial C_{0}}{\partial U(C_{0},C_{1})/\partial C_{1}} =(1+r)$

Relative price to the intertemporal utility optimization is given by $(1+r)$

Example of Intertemporal Choice - Adapting to Chronic Kidney Disease¶

Living with a dialyzer throughout life is an unpleasant experience.
When asked about willingness to live… where 1 means indifferent between such life and a healthy life and 0 means indifferent between such life and dying
- Healthy people's average: 0.32
- Current dialysis patients: 0.52
One potential reason: the reference scale changed… current patients forgot how good "perfectly healthy" feels like. Thus, their "1" is a healthy person's "0.6".
Another study: How would quality of life be after the kidney transplant?
- Who didn't receive transplants… were better off than they predicted
- Who did receive transplants… were worse off…
They don't really reason it out well!