Lecture 32 Hedonic Editing Hypothesis

Sairam

The Framing of Gains & Losses

• Lecture 26__The Value Function#
• KT's Value function
  1. \(v(\cdot)\) defined over perceived gains and losses relative to some natural reference point
  2. \(v(\cdot)\) assumed to be concave for gains, and convex for losses.
     • \(v''(x)\lt 0\) when \(x \gt 0\) (gains), has a maxima
     • \(v''(x)\gt 0\) when \(x \lt 0\) (losses), has a minima
  3. Loss function is steeper than the gain function
     • \(v(x) \lt -v(-x)\) for \(x\gt 0\) (gains)

       The value of gains is perceived smaller in absolute terms (-ve sign) than the same amount of loss.

Decision Frames

• Three ways of framing outcomes
  1. Minimal account
     • Focus remains on the necessary concept: "Am I willing to drive 20 minutes to save $5?". In this situation, he would be indifferent to either situations.
     • Focus only on the differences, not on the common features.
  2. Topical account
     • Relates consequences of the choices to a reference level
     • This ref level is determined by context
     • e.g. Mental Accounting
  3. Comprehensive account
     • Accounts for all factors
     • Current wealth, future earnings, possibility of other holdings etc.
     • Econ Theory assumes people use comprehensive account

• Jacket & Calculator Example

  • Let existing wealth be \(W\)
  • Let \(W^* =W +\text{Jacket + Calculator} - \$140\)
  • Then the choice is between
    • utility of \(W^* + \$\)
    • \(W^* + \text{20 mins}\)

  The way a decision is framed will not alter choices if using a comprehensive wealth-based analysis.

  • But framing does alter choices in the real world, people take decisions piecemeal, influenced by context of choice

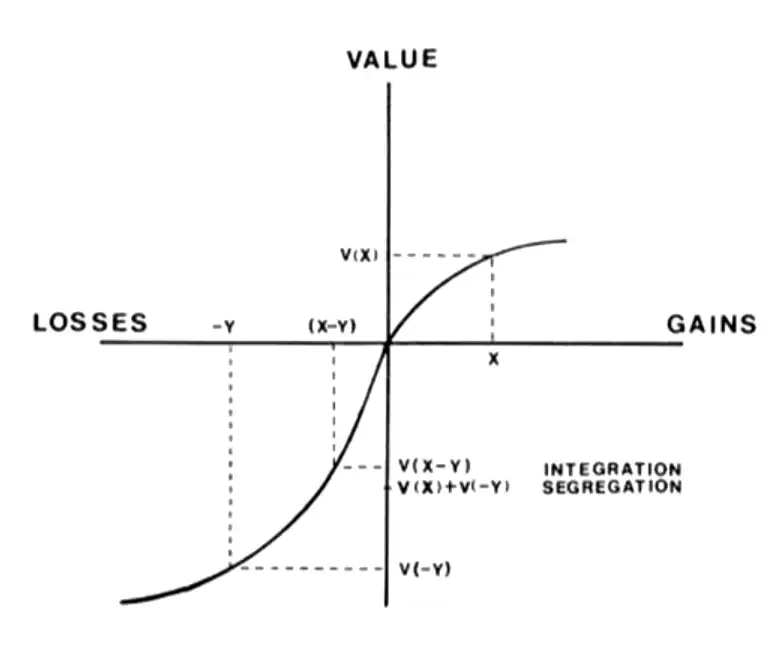
Coding Gains & Losses

• Value function defined over unidimensional outcomes
• What about joint outcomes \((x,y)\)? Two possibilities
  1. Value them jointly, integrated outcomes \(v(x+y)\)
  2. Value them separately, segregated outcomes \(v(x) + vx(y)\)
• Now, which one between these two produces greater utility?
• Why is this issue interesting?
  • If given the choice to code, they would frame outcomes in whatever makes them happiest
  • They have preferences of life organization, would they rather have salary + bonus or a salary equivalent amount?
  • (Marketing) how would the seller frame the characteristics of the transactions. Which to combine, which to separate?

Hedonic Framing

• Jacket & Calculator problem demos that MA is piecemeal & topical.
• We are more willing to save money on a small purchase than a large one.
• Disparity \(\implies\) \(v(-125) - v(-120) \neq v(-15) - v(-10)\)
• Now, how to combine two or more financial outcomes?

4 experiments & Theory they developed

• Segregation . + .
• Integration .

1. Mr. A : $50 in one, $25 in another
   • Mr. B single, larger World Series lottery: $75
   • \(A \gt B\), happier
   • Multiple gains: Segregation is preferred. \(v(x) + v(y) \gt v(x+y)\) (concave value function)

     Frequency tells you are lucky

2. Mr. A: $100 tax return, $50 state tax return, arithmetical mistake
   • Mr. B: Owed $150… no other repercussions in either case
   • \(A \gt B\) Upset… "Just hit once bro"
   • Multiple losses: Integration is preferred.
     \(v(-x) + v(-y) \gt v(-(x+y))\) (concave)

     Frequency tells you are unlucky

3. Mr. A won $100 in lottery and had to pay $80 to the landlord for an accident for the damaged rug.
   • Mr. B first lottery ticket… won $20.
   • \(B \gt A\), happier
   • Mixed Gain: Integration is preferred
     \(v(x) + v(-y) \lt 0\) while \(v(x-y)\gt 0\) when \(x \gt y\) (loss function is steeper)
   • Integration leads to cancellation**
4. Mr. A's car damaged \(\to\) $200 to repair…He won $25 in the office football pool.
   • Mr. B's car damaged \(\to\) $175 to repair.
   • \(B \gt A\), upset
   • Mixed Loss: Segregation is preferred
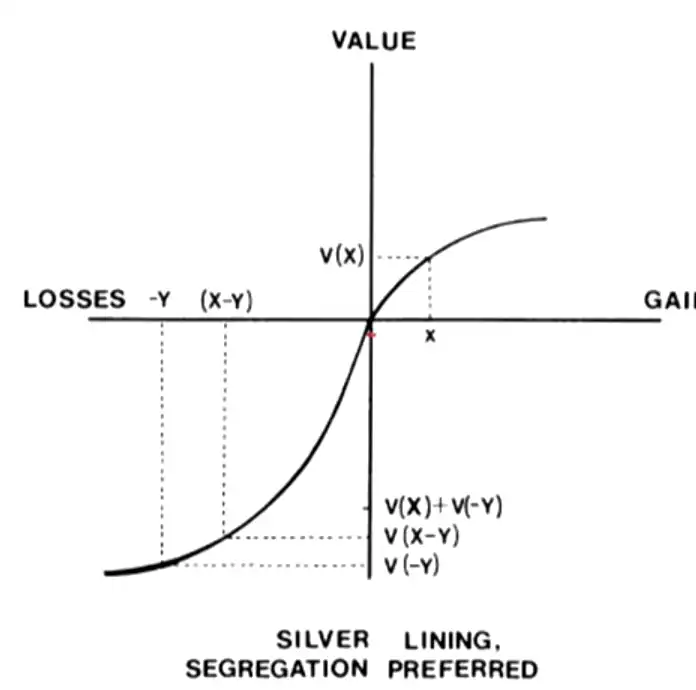
   • Silver Lining principle

Mixed Losses (close vs large gap)

• When \(X\) and \(Y\) are relatively close, integration is preferred
  
• When \(Y \gg X\), segregation is preferred (SILVER LINING EFFECT) \((-200 + 25)\)
  

Hedonic Framing

• Principles of hedonic framing, give us a way of evaluating joint outcomes
  1. Segregate gains (concave)
  2. Integrate losses (convex)
  3. Integrate smaller losses with larger gains (to offset loss aversion) \(\to\) Cancellation
  4. Segregate small gains (silver lining) from larger losses (gain function is steepest at origin, utility of a small gain \(\gg\) utility of slightly reducing a large loss)