Lecture 27 The Weighting Function
- Decision Weighting
- Don't interpret Decision weights as probabilities, measures of degree or belief
- Gamble: win 1000 or nothing. Toss fair coin: \(\pi(0.5) \lt 0.50\)
- Increasing function \(\pi(0)=0\to \pi(1)=1\)
- Scaled such that \(\pi(p)\) is the ratio: \(\dfrac{\text{Weight associated with probability }p}{\text{Weight associated with a certain event}}\)
- \(\pi(p) = p\) if expectation principle holds
- DW can be influenced by other factors, ambiguous
Three important axioms of \(\pi\) that violate normal probability axioms
- Subadditivity
- for small probabilities
- \(\pi\) is a sub-additive function of \(p\) \(\ni\) \(\pi(rp) \gt r\pi(p)\) for \(0 \lt r \lt 1\)
- \((6000, 0.001) \succ (3000,0.002)\) by 73%
- \(\pi(0.001)v(6000) \gt \pi(0.002)v(3000)\) owing to people's preferences
- By diminishing marginal sensitivity
- \(v(3000) \gt 0.5v(6000)\)
- since, \(2v(3000) \gt v(6000)\) by concavity
- \(\implies\) \(\pi(0.001)\cancel{v(6000)} \gt\) \(\pi(0.002)v(3000) \gt \pi(0.002)0.5\cancel{v(6000)}\)
- Or \(\pi(0.001) \gt 0.5\pi(0.002)\)
- \(\implies \pi(0.5 \times 0.002)\gt 0.5\pi(0.002)\)
- Here, \(p =0.002, r=0.5\)
- \(\implies\) normal risk-aversion for gains and diminishing marginal sensitivity doesn't hold for small \(p\).
- Overweighting Small Probabilities
- \(\pi(p) \gt p\) for small \(p\)
- \((5000,0.001)\succ (5)\)
- Prefer lottery ticket over the expected value of the ticket
- \((-5000,0.001) \prec (-5)\)1
- Can be seen as a payment of insurance premium
- Sub-certainty
- \(\pi(p) + \pi(1-p) \lt 1\) \(\forall\ 0 \lt p \lt 1\)
- Eventually we can show that, for Gamble C & D
- \(\pi(0.33)v(2500) \gt \pi(0.34)v(2400)\)
- \(\implies [1-\pi(0.66)] \gt \pi(0.34)\)
- So, \(\pi(0.66) + \pi(0.34) \lt 1\)
- slope of \(\pi\) in \((0,1)\) interval = measure of sensitivity of preferences to changes in probability
- So,preferences are generally less sensitive to variances of probability than the expectation principles
- Sub proportionality
- Recall
- If \((x,p) \sim (y,pq)\) then \((x,pr) \not\succ (y,pqr)\) for \(0\lt p,q, r \leq 1\)
- Or \(\pi(p)v(x) = \pi(pq)v(y)\) \(\implies \pi(pr)v(x) \leq \pi(pqr)v(y)\)
- Therefore, \(\dfrac{\pi(pq)}{\pi(p)} \leq \dfrac{\pi(pqr)}{\pi(pr)}\)
- For a fixed ratio of probabilities, ratio of corresponding \(\pi \to 1\) when probabilities are low than when they are high.2
- Example: \((3000) \succcurlyeq (4000,0.8)\) But with \(r=\dfrac{1}{4}\)
- \((3000, \dfrac{1}{4}) \succ (4000, \dfrac{0.8}{4})\)
- This is because people judge probabilities that are same in relative terms (e.g. 1 to 0.8 and 0.25 to 0.20 are the same relatively \(r=\dfrac{1}{4}\)) when they are smaller than larger. i.e. \(0.25\) is more similar to \(0.20\) than \(1\) is to \(0.8\).
- Example: \((3000) \succcurlyeq (4000,0.8)\) But with \(r=\dfrac{1}{4}\)
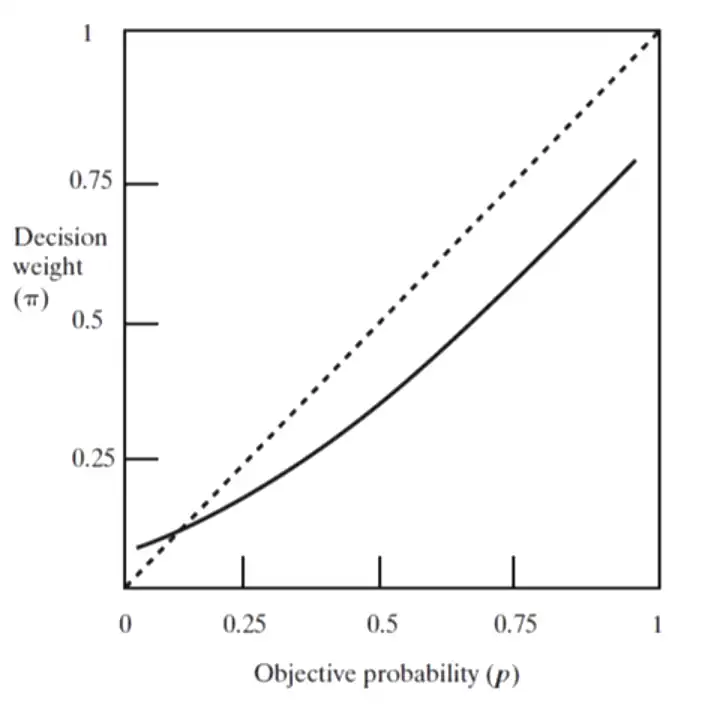A hypothetical function that satisfies overweighting, subadditivity for small values of \(p\) as well as sub-certainty and sub-proportionality. - \(\pi(p)\) is less steep than the \(45\degree\) line and discontinuous at both ends. A limit to how small a decision weight can be attached to an event.
- A small amount of doubt limits the upper end.
- Simplification of prospects \(\implies\) discard events with extremely low probability (zero weight). Ignored or overweighed due to lack of ability to evaluate.
- \(\pi(p) = f(p)\) when \(p\) is known to respondents
- \(\pi(p) = \dfrac{p^\gamma}{(p^\gamma + (1-p)^\gamma)^{1/\gamma}}\) where \(\gamma\) is the curvature of the value function.
- This function is a monotonic transformation of outcome probabilities: \(f \neq g\) and \(f(s) \geq g(s)\) \(\forall s \in s\) \(\implies\) \(f\gt g\)
- Two problems with this function form: ^2432a8
- doesn't satisfy Stochastic Dominance
- Cannot be readily extended to prospects with large number of outcomes. ^48580b
- Recall