doubt In PT, are the outcomes mutually exclusive?¶

The Value function
- Carrier of value = change in wealth or welfare¹
- e.g. our response to attributes like brightness, loudness or temperature, past experience contexts, defines an adaptation level or reference point
  - An object is felt based on the feeling one has already adapted to.²
- Same principle applies to non-sensory attributes like health, prestige and wealth
- Strictly: value = $f(\text{Asset position},\text{Change})$
- However, preference order is not altered by variation in asset position
  - Certainty equivalent of $(1000,0.5)$ lies between $300$ and $400$ (when it should have been $500$) in a wide range of asset positions.
  - $\implies$ Approximation: ignore the asset position and only take change, will give a satisfactory approximation.
- Many sensory and perceptual dimensions share:
  - psychological response is a concave function of magnitude of physical change³
  - e.g. $3\degree$ vs $6\degree$ is easier to discriminate than $13\degree$ vs $16\degree$
- Similarly
  - Difference in gain of $100$ vs $200$ appears to be significant when compared to $1100$ vs $1200$
  - And difference in loss of $100$ vs $200$ appears to be significant when compared to loss of $1100$ vs $1200$ unless the larger loss is intolerable
- $\implies$ Value function for changes in wealth
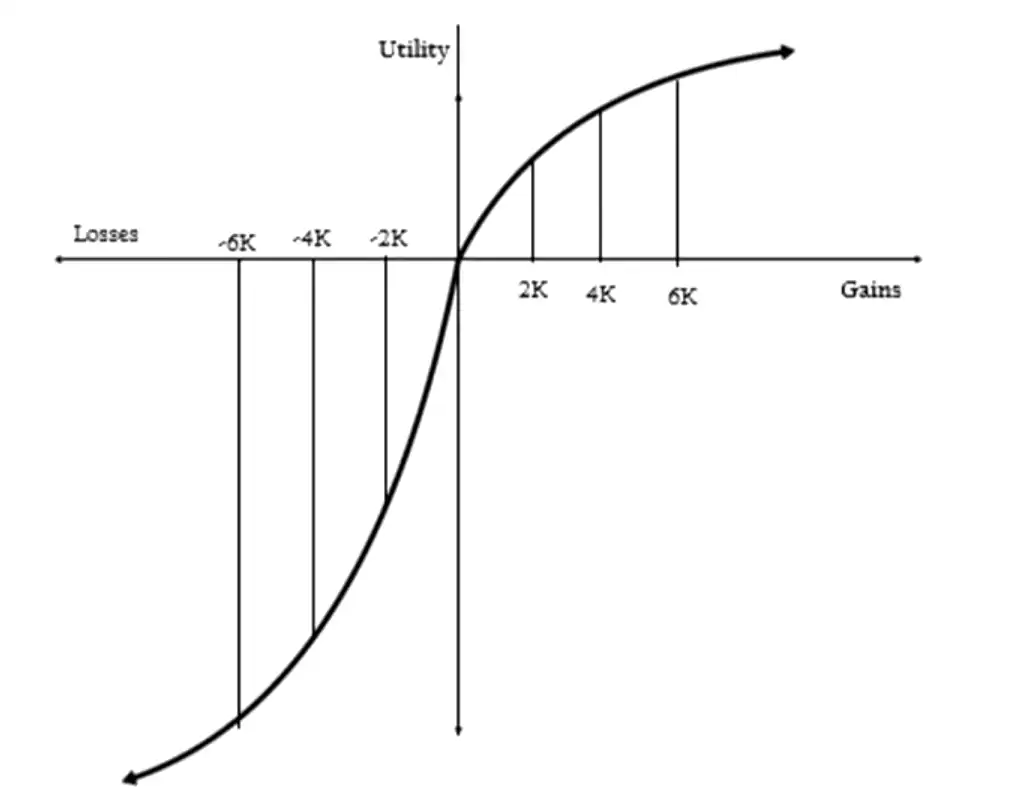
  - concave above reference point ($v''(x) \lt 0$ for $x\gt 0$)
  - convex below it ($v''(x) \gt 0$ for $x \lt 0$)
  - Marginal value of gains and loss generally decreases with their magnitude
- Value functions derived from risky choices shares the same characteristics
  - doubt In PT, are the outcomes mutually exclusive?¶
  - The following prospects, $A$ vs $B$ and $C$ vs $D$
    
    Gamble Prospect Votes
    
    A $(6000,0.25)$ 18%
    
    B $(4000, 0.25; 2000, 0.25)$ 82%
    
    C $(-6000, 0.25)$ 70%
    
    D $(-4000, 0.25, -2000, 0.25)$ 30%
  - $\pi(0.25)v(6000) \lt$ $\pi(0.25)[v(4000) + v(2000)]$
  - $\pi(0.25)v(-6000) \gt$ $\pi(0.25)[v(-4000) + v(-2000)]$
  - So, $v(6000) \lt v(4000) + v(2000)$ (Concave)
  - And $v(-6000) \gt v(-4000) + v(-2000)$ (Convex)
    - Utility function should leave room for special circumstances' effects on preferences
    - Person who needs $\$60,000$ to buy a house, will reveal an exceptionally steep rise in utility near the critical value.
  - Similarly, aversion to losses may increase sharply near the loss that is intolerable (compels him to sell his house)
    - $\implies$ Derived value function of an individual doesn't reflect "pure attitudes to money" (as it is affected by additional consequences)
  - These create convex regions in value for gains and concave regions in value for losses
    - K&T propose that Value function is
  - Defined on deviations from reference point; $0$ is the reference point in this case
  - concave $\to$ gains. convex $\to$ losses⁴
  - steeper for losses than for gains⁵
    - If $x \gt y \gt 0$ (proof for (3))
  - $\implies v(y) + v(-y) \gt v(x) + v(-x)$
  - For $y=0,$ $-v(-x) \gt v(x)$
  - Let $y$ approach $x$ $\to$ $v'(-x) \gt v'(x)$
    - K&T focus on changes:
      
      "Chances are the way Humans experience life"
  - Say someone is earning 80000 and gets a 5000 bonus. According to Neoclassicals, it may not be a big amount as this is a one-time thing and when compared to the lifetime wealth expectancy, it is nothing.
  - However, when she compares it to her current scenario, she says "Wow! An extra 5000!"
  - Empirical Evidence
    - Detailed analysis of von Neumann-Morgenstern utility functions for changes to wealth
    - Functions obtained from 30 decision makers (5 independent studies)
    - Observations
  - most gains were concave
  - most losses were convex
  - only three individuals exhibited risk aversion for both gains and losses
  - except one, utility was considerably steeper for losses than for gains

Consistent with the basic assumptions of perception or judgement ↩
E.g. Dip each of the hands in hot and cold water, and then dip both hands in the same lukewarm water. Both get a different sensation ↩
I.e. it is felt harder at extremes but not in intermediate points ↩
Diminishing marginal sensitivity $\implies$ risk-aversion in gains, risk-seeking in losses ↩
Losses loom larger than gains. One experience from losing has a greater aggravation than the pleasure of gaining the same amount $\implies$ most people find symmetric bets distinctly unattractive. aversiveness increases with the size of the stake. ↩

Gamble	Prospect	Votes
A	\((6000,0.25)\)	18%
B	\((4000, 0.25; 2000, 0.25)\)	82%
C	\((-6000, 0.25)\)	70%
D	\((-4000, 0.25, -2000, 0.25)\)	30%