Skip to content

Sairam

Continuing after Lecture 22__Risk Attitude & Axioms of EUT#^be6d07|5. Monotonicity

  1. Substitution Axiom ^953478
    • \(B \succ A \implies\) \((B,p) \succ (A,p)\)

Some violations

  • Certainty Effect
    • A violation of (6) is Certainty effect: People overweight outcomes that are considered certain, compared to probable ones.
    • Counter-example 1953: Maurice Allais, French #economist
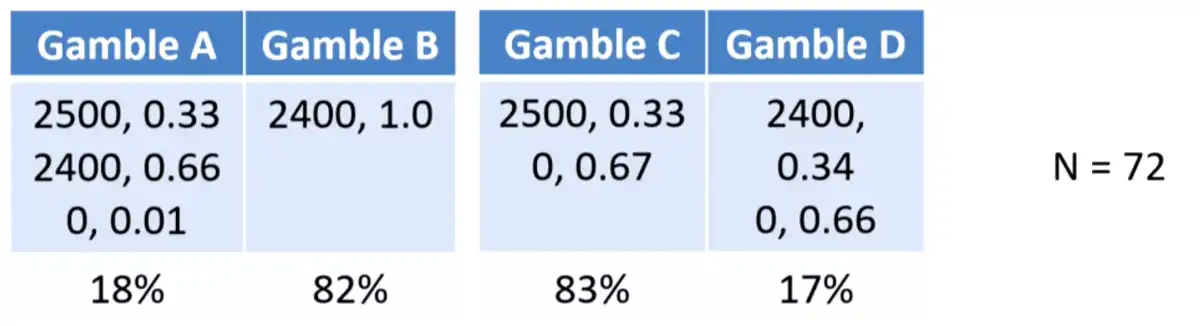
      • 18% since \(u(0) =0\)
      • Response: \(B \succ A\)
        • \(\implies u(2400)\gt\) \(0.33u(2500)+0.66u(2400) +0\)
        • So, \(0.34u(2500) \gt 0.33u(2500)\)
      • The second preference: \(C \succ D\)
        • \(\implies 0.33u(2500) \gt 0.34u(2400)\)
        • But this contradicts what we found in the first response! (\(B \succ A\))
      • There is preference reversal!
    • When there is uncertainty, then people prefer things differently.
    • \(\implies\) There is always a greater preference for a prospect with certainty
    • Certainty effect is valid for non-monetary outcomes as well (N=72)
      • \(A:\) 50% chance (3-week tour) England, France & Italy
      • \(B:\) With Certainty one-week tour of England
      • 78% chose \(B\)
      • \(C:\) 5% chance to win a three-week tour of England, France & Italy
      • \(D:\) 10% chance to win a one-week tour of England
      • 67% chose \(C\) even though the odds1 remain the same. The fact that both events are uncertain led the majority chose one with greater rewards (the 3-week tour).
  • The Common Ratio Effect - Probability & Possibility
    • \(A = (6000,0.45)\) vs \(B = (3000,0.90)\)
      • People choose \(B \succ A\), where winning is more probable (\(0.90 \gt 0.45\))
    • \(C = (6000, 0.001)\) vs \(D = (3000,0.002)\)
      • People choose \(C \succ D\). Since between \(C\) and \(D\) winning is possible but not probable. Most people choose the prospect that offers the larger gain.

  • The Reflection Effect

    • E.g. \(A: (4000,0.8) \prec (3000)\) (Certainity effect, N=95)
      • But \(A': (-4000,0.8) > (-3000)\)... A larger loss with some probability was preferred to a certain loss.
    • E.g. \(B: (4000, 0.2) \succ (3000,0.25)\) (Common Ratio Effect, N=95)
      • But \(B': (-4000,0.2) \prec (-3000, 0.25)\)... Prefer a smaller loss which is more probable to a larger loss (if they are both possible but less probable, "The worst that can happen is that I incur a loss, but at least I will save 1000")
      • Similar to: \(D: (3000,.002) \prec (6000, 0.001)\) and \(D': (-3000,0.002) \succ (-6000,0.001)\): reflection effort.
    • Risk aversion in the positive domain is accompanied by risk seeking in the negative domain. In \(A': (-4000,0.08)\) has expected value \(-3200\) but is preferred to a sure loss of \(3000\). People are willing to take the risk if it has even a slight chance to save them.

    • study by Williams:

      • \((100, 0.65; -100, 0.35) \sim (0)\) : risk aversion
      • \((-200, 0.08) \sim (-100)\) : risk seeking

    • Note that the correspondence is inconsistent with EUT. \(|-3200| > |3000|\). Outcomes which are obtained with certainty are overweighed

      • Positive domain: risk averse
      • Negative domain: risk seeking (for a loss that is merely probable \(\gt\) smaller loss that is certain)

      Psychological Principle2 Overweighing of certainty favors risk aversion in the domain of gains and risk seeking in the domain of losses.

    • To resolve the inconsistency, assume "People prefer prospects that have higher expected value and smaller variance"

      • \((3000)\) has no variance so it is preferred even if smaller expected value
      • When prospects are reduced, the difference in variance between \((3000, .25)\) and \((4000, .20)\) may be insufficient to overcome the difference in expected value.3
      • But according to this \((-3000)\) has both higher expected value (lower loss) and lower variance... but data says otherwise...
      • SO THIS IS NOT REALLY THE RIGHT ASSUMPTION
    • \(\implies\) Reflection Effect\(\implies\) Certainty
      • increases aversiveness of losses
      • increases desirability of gains
    • Another experiment:
      • You have been given 1000 and asked to choose:
        • \(A: (1000, 0.5)\) & \(B: (500)\)
      • You have been given 2000 and asked to choose:
        • \(C: (-1000, 0.5)\) & \(D: (-500)\)
      • \(B \succ A\) and \(C \succ D\) (consistent with Reflection effect)
      • But note that both choices are identical in terms of final states
      • The pattern of results is inconsistent with utility theory which says that wealth of 100,000 is assigned the same utility, regardless from a prior wealth of 95,000 or 105,000. (Which is contradictory here)
    • \(\implies\) Carriers of Utility are "changes of wealth" rather than the "final asset positions"
    • Interestingly, an avid buyer of insurance may not be covered for many other perils, in a contingent insurance. Yet, perceives a probabilistic insurance as more risky.

  1. The ratio of probabilities ↩

  2. People try their luck to avoid losses. But they don't want to try their luck in the case when they can gain something (perhaps, because the pain of losing something is something that they would wish to avoid at all cost) ↩

  3. So, do people actually think statistically? ↩