Lecture 22 Risk Attitude & Axioms of EUT

Sairam

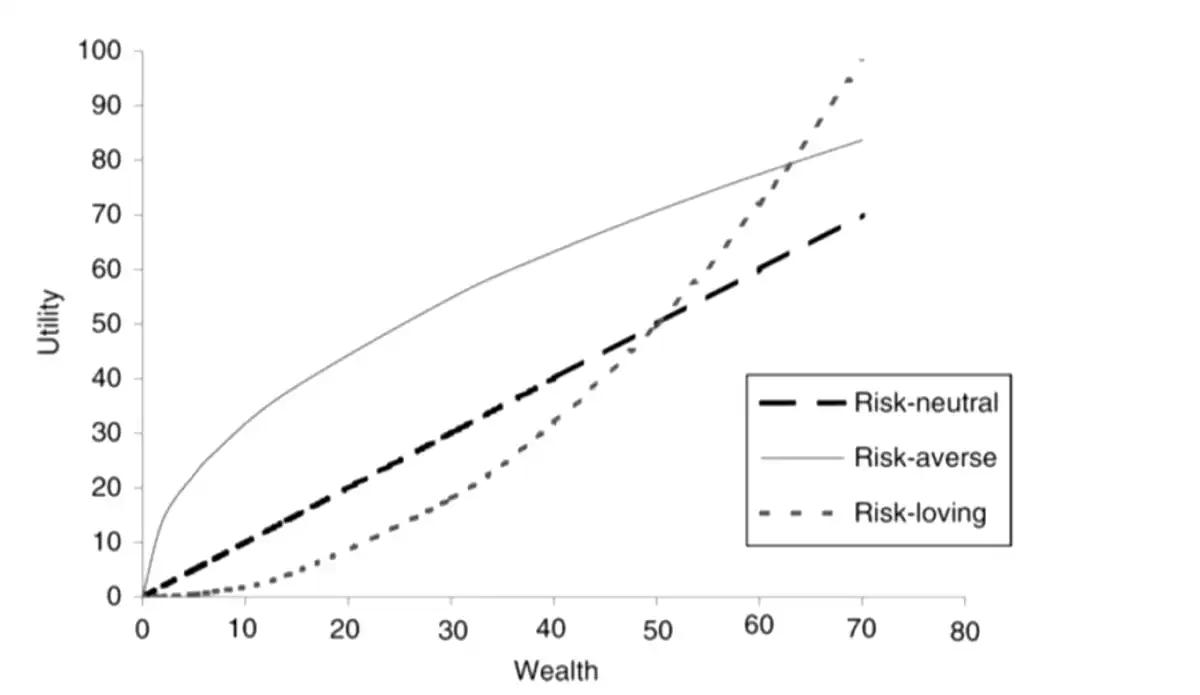
Attitudes Towards Risk¹
Risk Aversion
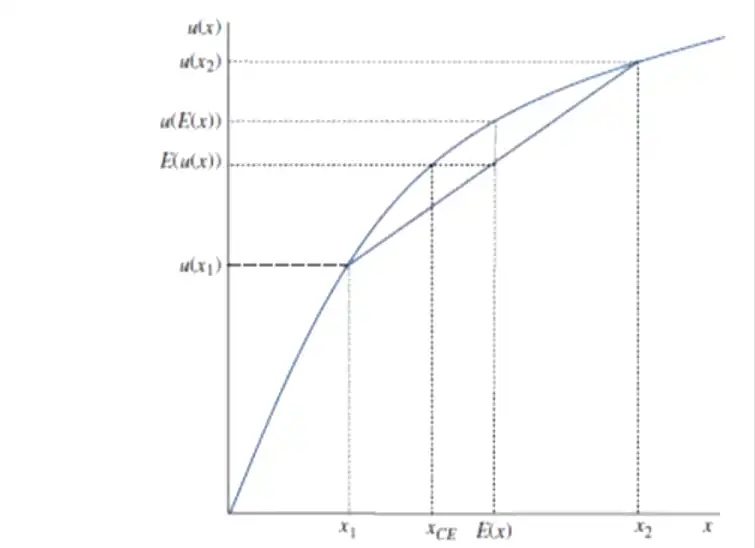
- Prospect: \((x_{1},0.5;x_{2},0.5)\)
- \(E(x) = 0.5x_{1} +0.5x_{2}\) is exactly equidistant from \(x_{1}\) and \(x_{2}\) on the horizontal axis.
- Vertical axis: \(u(E(x)) = u(0.5x_{1}+0.5x_{2}) \gt E(u(x))\) \(= 0.5u(x_{1}) +0.5u(x_{2})\)
- So, \(u(E(x)) \gt E(u(x))\)
  - \(E(u(x))\) is halfway through \(u(x_{1})\) and \(u(x_{2})\)
  - \(E(x)\) is halfway through \(x_{1}\) and \(x_{2}\)
  - "Slope of \(u\) between \(E(x)\) and \(x_{2}\)" \(\lt\) "Slope between \(x_{1}\) and \(E(x)\)"
- Due to diminishing marginal utility. Utility increases at a decreasing rate > As one has more wealth, they would become more risk averse. That's why associates a lower amount of utility to \(x_{2}\) than \(x_{1}\)
- Definition: \(x_{CE}\) is the certainty equivalent since, \(u(x_{CE}) = 0.5u(x_{1}) + 0.5u(x_{2})\). Yields the same level as expected utility of the gamble, \(E(u(x))\)
  - \(x_{CE} < E(X)\) reflecting that the person is willing to give up some amount of money (on average) in in return for certainty. #doubt How does it reduce uncertainty?

The Axioms of EUT¶

We will look at axioms and their violations as observed by behavioralists.

Preference symbols: - \(\succ :\) preferred to - \(\sim :\) as good a - \(\succcurlyeq:\) at least as good as

Completeness
- \(\forall A,B\)
- \(B \succ A\) or \(A \succ B\) or \(A \sim B\)
Transitivity
- for three prospects \(A,B,C\)
- \(A \succcurlyeq B\), \(B \succcurlyeq C\) \(\implies\) \(A \succcurlyeq C\)
- Order or Ordering Axiom
- Intransitive Preference: Preference Reversal
  - \(E = A \succ F=C \succ D=B \succ A\)
  - \(\implies A \succ C \succ B \succ A\)
Continuity
- If \(A \succ B \succ C\) then \(\exists\) probability \(r\) \(\ni\)
  - \(rA + (1-r)C \sim B\)
  - The prospects \((B)\) and \((A,r;\ C, 1-r)\) are indifferent
  - The latter is a Compound Prospect
- For any \(p > r\)
  - \(pA + (1-p)C \succ B\)
  - and vice-versa (\(p < r\))
Independence ^3a00a1
- Definition: \(\forall A,B,C\) if \(A \succ B\) then,
  - \((A,p; C,1-p) \succ (B,p; C, 1-p)\) \(\forall p\)
  - i.e. \(C\) doesn't affect the compound prospect's preference order
- e.g. \(\text{Coffee} \succ \text{Tea}\) and \(P(\text{Rain} )=0.6\)
  - Regardless of rain or not, my preference for coffee over tea will not change
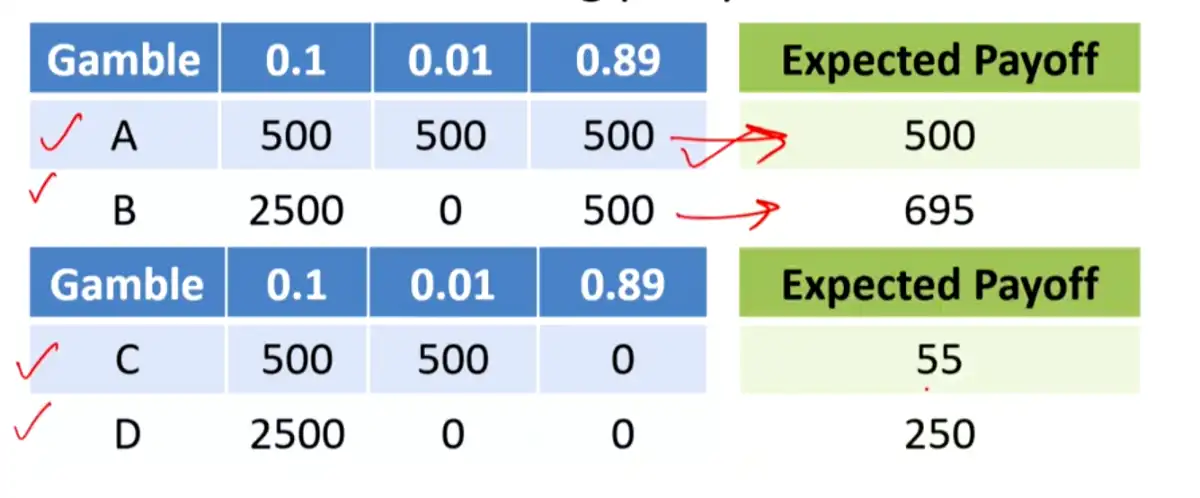
- e.g. K&T If the probabilities are reduced in equal proportion:
  - \(A = (3000) \succ B = (4000,0.8)\) then,
  - \(A'=(3000,0.25)\) should be \(\succ B'=(4000,0.2)\)
  - Here, \(C = 0\) and \(p = 0.25\)
- However, K&T found that about 80% of those asked, chose \(A \succ B\), and about 65% would choose \(B' \succ A'\). - #violation!
- Isolation Effect: Another #violation
  - \((0,0.75; \text{Stage 2}, 0.25)\)
  - Stage 2: \((4000,0.8)\) vs \((3000)\)
```
graph LR
    A((Chance: End?)) -->|1/4| B["Choice"]
    A -->|3/4| Z["0"]
    B --> C(("Chance"))
    C -->|4/5| E[4000]
    C -->|1/5| F[0]
    B --> D[3000]
```
  - In terms of final outcome: the choice is between
    - \((4000, 0.2)\) and \((3000,0.25)\)
    - 78% chose the latter prospect: \((3000,0.25)\)
    - Contradicts: Just the previous K&T (65% people preferred)
  - Evidently, the reason is:
    - People ignored the first stage of the game
    - Considered it a choice between \((3000)\) vs \((4000,0.8)\)
    - "Anyway, the first chance is not in my hands... If I get through, I should not miss the chance." "But wait, if you actually get through the first stage, don't you think you are testing your luck too much by choosing an uncertain option? I mean you are talking about a situation which even more improbable"
  - \(\implies\) Choices are primarily determined by the probabilities of the final state (in isolation)
- Common Outcome Effect:
  - \(A \succ B\) and \(C \succ D\)
  - If the third column is removed in both then the gambles \(A,C\) are identical and \(B,D\) are identical (with the probabilities)
  - But it was observed, \(A \succ B\) and \(D \succ C\). VIOLATION! Actually not independent!
Monotonicity ^be6d07
- Let \(x_{1},x_{2}\dots x_{n}\) be outcomes ordered from worse \((x_{1})\) to best \((x_{n})\)
- Prospect \(q\) stochastically dominates \(r\) ^6eeac7
- If at least one \(p_{qj} > p_{rj}\) #doubt ==I don't understand what it means. Can the situation be explained please?==
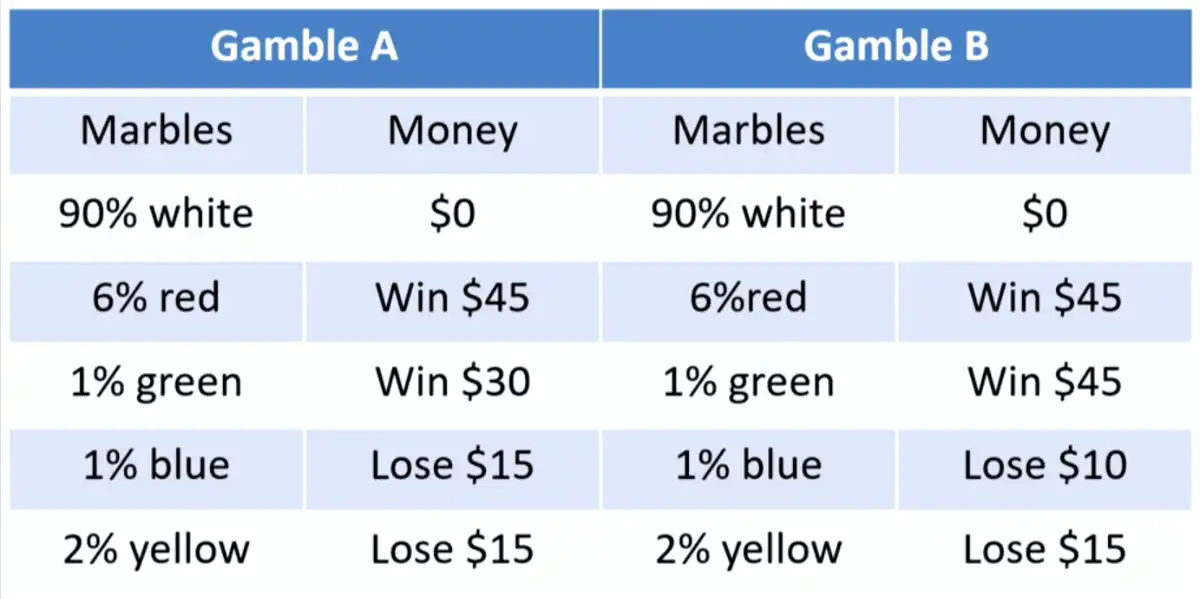
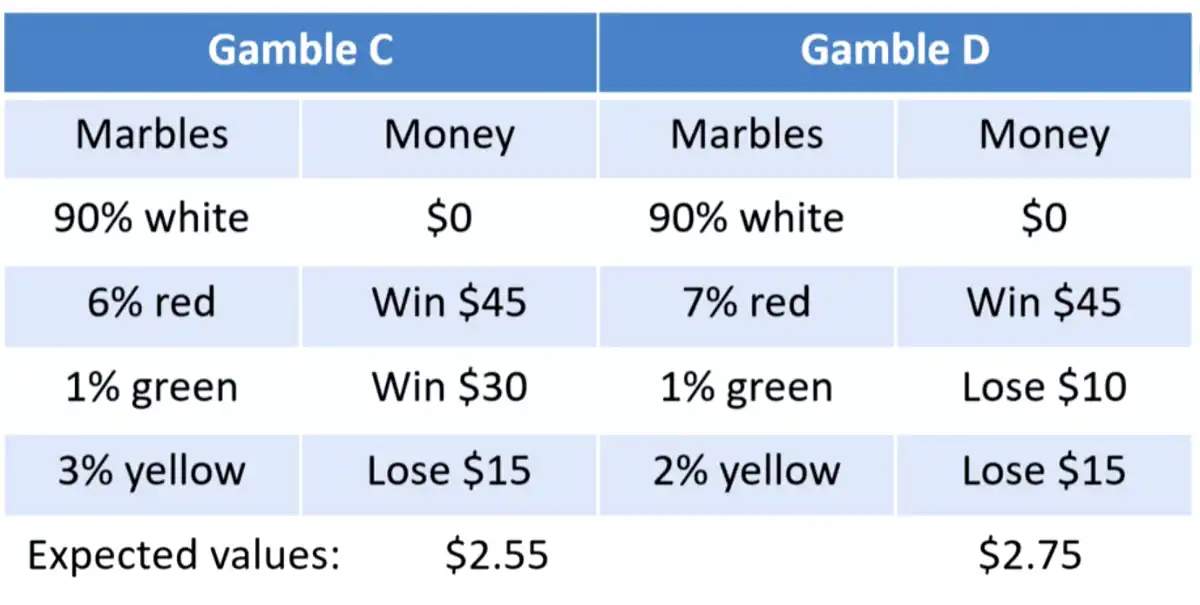
- - People preferred \(B \succ A\)
- VIOLATION:
  - Out of 124 people, K&T found 60% to prefer: \(C \succ D\)
  - Though \(A \sim C\) and \(B \sim D\) and thus people should have: \(D \sim C\)
- Reason: People focus on the options more than the probabilities. They look at the gamble with the least number of losses and thus select \(C\).
  - Due to lack of transparency in presentation of the gamble.

Convex or concave to the horizontal axis ↩