Lecture 20 Bayesian Updating and Confirmation Bias
- Bayesian Updating
- Update beliefs in light of new evidence
- In science, Update assessment about plausibility of a hypothesis or theory in light of evidence (from experiments, field studies, other sources)
- \(H:\) Hypothesis. \(E:\) Evidence.
- \(P(H)\) is prior. \(P(H|E)\) is posterior probability. (Given Evidence \(E\) is TRUE)
 Narrowing down
Narrowing down- Use Bayes' Rule to determine posterior.
- If changing belief according to Bayes' rule, we say we engaged in Bayesian updating
- "Two heads" or Fair coin Example
- \(H:\) The coin has two heads.
- Prior: \(P(H) = 0.01\) (say)
- \(E:\) A head comes up.
- \(P(E|H) = 1\) and \(P(E|\neg H) = 0.5\)
- \(P(H|E) = 0.02\) (first Update)
- \(P((H|E)|E) =0.04\) (second Update)1
- This is called Bayesian updating
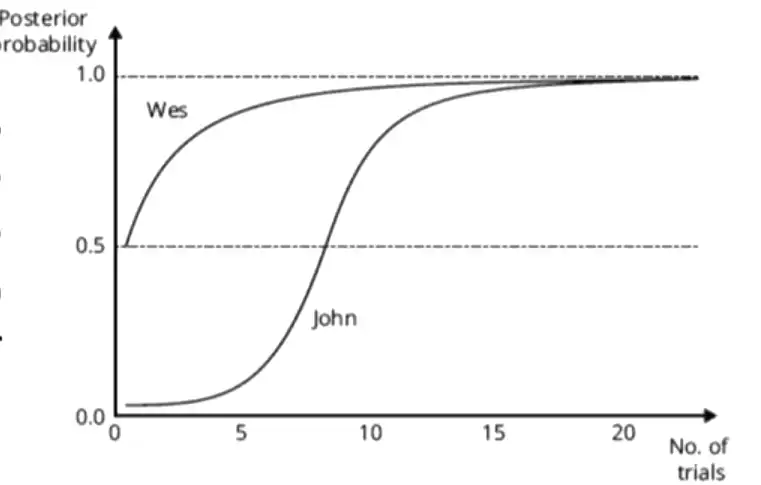
- \(H:\) The coin has two heads.
- Washing out of Priors
- After 15 flips: \(P(H) = 100\%\) (refers to "Washing out of Priors")
- John and Wes roughly assign the same probability, independently of what each of their priors used to be.
- Rational people exposed to the same evidence: come to agree regardless of their initial stance
- IRL doesn't happen. Reasons:
- Very different evidence (e.g. conservative newspapers/blogs, selected information)
- Confirmation Bias
- Confirmation Bias
- Tendency to interpret evidence as supporting prior to a greater extent than warranted. \(P(H|E)\) will grow slower than rational if I see \(E\), and my prior belief was that the coin was unbiased.
- Death Penalty
- Two groups (for or against)
- Same information provided (neutral)
- Instead of coming to an agreement or the same conclusion... they strongly supported their prior beliefs
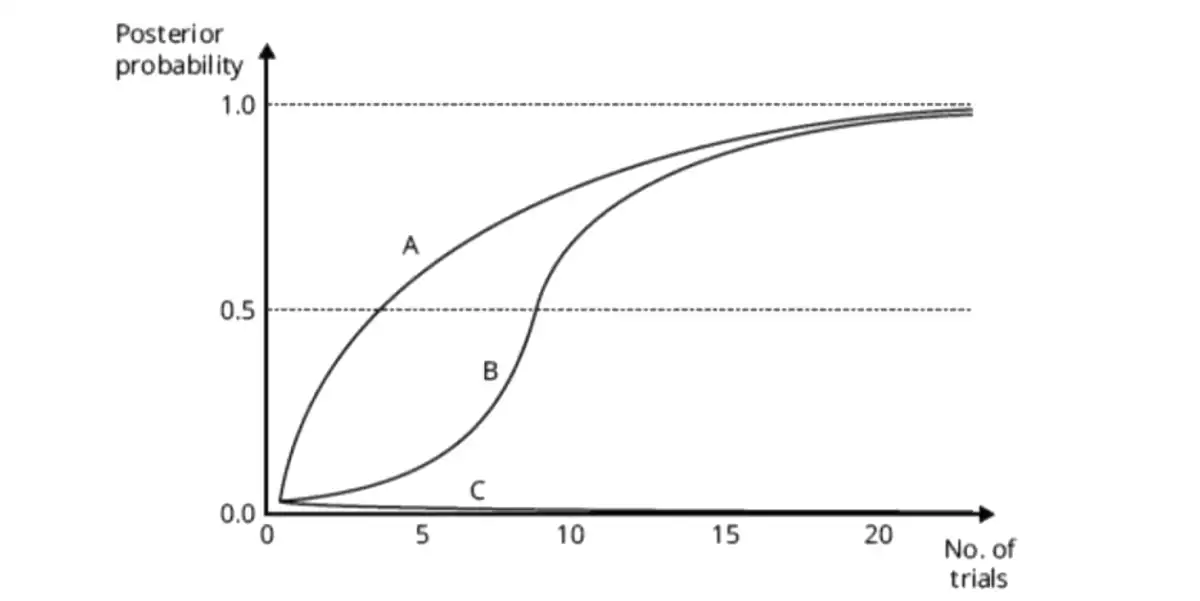
- Individuals \(A\), \(B\) and \(C\)
- A and B are rational, with different priors and agreed to the same point at the end
- C doesn't budge, confirmation biased. He doesn't update his beliefs.
- Individuals \(A\), \(B\) and \(C\)
- Explains why racist and sexist stereotypes exist
- Sexist: Downplay evidence of girls being good at math and men being able to take care of children, but pick on quickly where they are not.
- Racist: notices all people of other races going good, but focus on only those who do not.
- Explains Gambling:
- Belief: "I can predict"
- Evidence: "You cannot"
- Result: "I can still predict" (irrational)... He will notice all the cases where he did predict correctly.
- Explains why people (think they) can beat the stock market
- Explains How conspiracy theories survive in spite of overwhelming contradictory evidence (credit: conspiracy theorist who puts weight on morsels of evidence)
- PhD Karl Popper: Scientists find evidence that support their theory everywhere.
- It is easy to "confirm" just any theory.
- Factors that contribute to confirmation bias:
- People sometimes fail to notice evidence that goes against their beliefs.
- Evidence vague \(\implies\) interpretation required. So, people tend to interpret in a way that supports their beliefs
- Tend to apply a much higher standard of proof to evidence contradicting their beliefs than otherwise.
-
Note that after two flips and getting a head, the probability increases faster than the previous update ↩