Endogenous Growth Models

Learning-By-Doing (The Arrow Model)¶

Endogenous Growth models: Learning - By- Doing (The Arrow Model):
Kenneth Arrow used the concept of learning-by-Doing (when a worker's productivity increases through Practice) to refer to skills acquired by hands-on work and not certified by the formal system of education.
Arrow used this concept to explain the effects of innovation and technological change on output and Productivity.
The eco. implications of "L-b-D": In his classical paper Published in 1962, he demonstrated that the increase in PCY can't be entirely explained by increase in K/L ratio.
He isolated the rate of technological change in economic growth by incorporating a separate term for knowledge in the Production Function and showed that how this contributes to the highest share of Overall productivity increase.
Arrow's research showed that differences in technology and Available labor significantly affect how fast a Country grows economically. He made govt. recognize that investing in education and R&D is vital for long-term growth.

Learning, Diminishing Returns, and Technological Progress¶

Arrow Observed that learning takes place by an attempt to solve a problem. Here, it takes place Only during an activity.
However, Arrow observed that learning with repetitive activities always yields diminishing returns.
Therefore, to have a steadily increasing performance, the challenges or tasks must evolve. They must become Complex or different, not just repeat.
Arrow also emphasized the role of experience in increasing productivity. As individuals produce goods, ways of improving Production processes happen inevitably.
The improvement in production as a by-product of normal production activity and not as a result of deliberate efforts.
Therefore, L-b-D can be recognized as the source of technological progress.
It is not merely The share of GDP allocated to R&D that drives Knowledge accumulation, but more crucially the extent to which new knowledge is indigenously created Through ongoing production activities in the economy.

The Production Function and Endogenous Knowledge¶

The production function, depending on the Technology accumulation will have the form of:

\[Y_{t}=K_{t}^{\alpha}(A_{t}L_{t})^{1-\alpha}\]

\(K\) capital, \(L\) Labor, \(Y\) output, \(A\) Stock of Knowledge and \(\alpha\) is a parameter lies bet 0 to 1.
The simplest case of L-b-D is found in those situations where learning occurs as a consequence of the Production of new capital.
Since increase in Knowledge = f(increasing capital) \(\rightarrow\) Stock of knowledge \(\propto\) f(stock of Capital).
As Capital is endogenous here, which grows through Savings and investment decisions, Since Knowledge is a function of stock of capital, via this knowledge also becomes endogenous.

\[A_{t}=BK_{t}^{\beta}\]

where \(\beta\) and \(B\) are positive.

\[Y_{t}=K_{t}^{\alpha}B^{1-\alpha}K_{t}^{\beta(1-\alpha)}L_{t}^{1-\alpha}.\]

where
- \(K_{t}^{\alpha}\) has direct contribution to output.
- \(K_{t}^{\beta(1-\alpha)}\) has indirect Contribution. This is the additional benefit of capital through its role in generating knowledge.
Final Production function is \(Y_{i}=A(K)F(K_{i},L_{i})\). It captures how an individual firm's output depends not just on its inputs but also economy wide capital stock, which enhances productivity Through L-b-D. Overall capital in economy will spillover.

The Romer model: Learning by Investment¶

Romer in his paper on endogenous growth Published in 1986 Presented a variant of Arrow's Model naming it as "learning by investment".
He considered knowledge as an input in the Production Function indicating:

\[Y_{i}=A(R)F(K_{i},L_{i})\]

Agg. Output \(A(R)\) - Public stock of knowledge from R&D
\(R_{i}\) - stock of returns from expenditure on R&D by firm (\(i\))
\(K_{i}\) - Capital stock of firm(\(i\)), \(L_{i}\) - Labor input of firm (\(i\))
Romer Considered the 3 key elements in his model:
- Positive externalities
- Increasing returns in the Production function of output
- Diminishing returns in the production of new knowledge

Knowledge as the spillover effect from R&D efforts or investment by a firm.¶

The effect of new research and technology acquisition by a firm was assumed to spill-over across the entire economy.
Therefore, in this model, new Knowledge is considered the key determinant of long-run growth which is determined by investment in research and new technology.
Romer separates the economy into 2 sectors:
- Goods sector: Uses capital and labor to produce output (Y).
- Research Sector: Uses labor and knowledge to produce a new Knowledge.

Returns, Externalities, and Monopoly Power¶

The implication of R&D exhibiting diminishing returns meant that investment in R&D will not therefore Continue to yield proportionate increase in Knowledge, thereby limited returns.
However, Other firms also benefit from new technology due to factor like inadequacy of Patent Protection.
In a Competitive equilibrium: firms act independently, aiming to max profit in a Competitive market.
This will result in positive externalities where one firm's innovation benefits other firms.
This leads to higher aggregate economy-wide returns. So, Romer's model explains how knowledge accumulation by profit - maxing firms, though it may yield limited returns at the individual level, creates Positive externalities That result in increasing returns to the entire economy.

The AK Model of Growth¶

O. Sergio Rebelo (1991) introduced the AK Model building upon The earlier work by Romer, the Ak model was simply expressed as Y = AK where \(A\) - Technology, \(K\) - Physical and Human Capital.
In this model there are no diminishing returns bcoz, the MPK is never negative.
Capital is assumed to have accumulated by some portion of aggregate output saved by individuals.
Capital accumulation (\(\dot{K}\)) is:

\[\dot{K} = sY - \delta K\]

Here, Capital will continue to grow since investment in this model is greater than depreciation.
This is bcoz
1. \(sY\) and \(\delta K\) are both linearly upward sloping lines.
2. Saving \(sY\) is a Constant function of \(Y\)
3. \(Y\) is linear in \(K\).

So, dividing both sides by \(K\):

\[\frac{\dot{K}}{K} = \frac{sY}{K} - \delta\]

and since \(Y = AK\)

\[\frac{\dot{K}}{K} = \frac{sAK}{K} - \delta\]

\[\frac{\dot{K}}{K} = sA - \delta\]

Here \(A\) is constant at this stage (\(A\) is fixed and growth comes from capital accumulation)

Taking \(\ln\) to growth equation,

\[ \ln Y = \ln A + \ln K \]

Differentiating w.r.t time,

\[\dfrac{\dot{Y}}{Y} = \dfrac{\dot{K}}{K}\]

Using this in \(\dfrac{\dot{K}}{K} = sA - \delta\):

\[\dfrac{\dot{Y}}{Y} = sA - \delta\]

\(\therefore\) Growth rate of output is an increasing function of the rate of investment (\(sA\)).

AK Model Growth Rate and Ideas as the Engine¶

We understood from the Solow model, that it is the technology that causes the investment in the capital which causes the actual growth.
Without technological change, growth would stop.
Therefore, one must Consider technology as a key driver to EG (Endogenous Growth).

How this technology grows in any economy?¶

It is the generation of new ideas, and the ideas themselves improve the technology of Production.
Romer in 1986, 1990 Papers modelled ideas as an engine of growth.
Romer's basic argument was that idea, as a good, was non-rivalrous in nature.
This made Romer suggest that this implies Increasing Returns to Scale (IRS).
If IRS to be present in a competitive environment we need an explicit representation of its research.
This also introduces the element of imperfect Competition.
The non-rivalrous goods need to be produced only once. Such goods have a fixed cost of production and Zero Marginal Cost (MC).
It takes a lot of effort to bring out the first unit of software, but subsequent copies are produced by just Copying from the first unit.
Nature of costs involving non-rivalrous goods suggest the presence of IRS and imperfect competition.
Why Non-rivalry leads to IRS?
- One time fixed cost to develop the idea (software).
- Very low or zero MC to make additional copies (download).
- Doubling input more than double the output (Since the idea is reusable).
This implies IRS.

Imperfect Competition and Patents/Copyrights¶

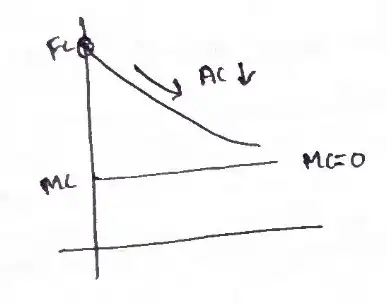
Under perfect competition, Firms charge Price = MC.
But here MC is 0.
If they price at \(MC = 0\), they can't recover The costs \(\pi = (P - AC)Y\).
With IRS \(AC > MC\).
When the producers get the power of patents and Copyrights they get monopoly powers for some time allowing them to reap profit from their ideas.

Robert Lucas and Human Capital¶

Robert Lucas utilized a model of endogenous growth developed by Uzawa.
Uzawa developed an endogenous growth model based on investment in Human Capital (HC).
Lucas also drew from the Theory of Human capital by Gary Becker.
Lucas assumed that investment on education leads to the production of human capital which is the crucial determinant in the growth process.
He classified this as:
- Internal effects of HC where the individual worker undergoing training becomes more productive.
- External effects: which spillover and increases the Productivity of capital and of other workers in the economy.
It is the investment in HC rather than PC that have Spillover effects that increase the level of technology.
Output for firm(\(i\)) takes the form:

\[Y_{i}=AK_{i}(H_{i})(\bar{H}^{e})\]

\(A\) - Technology coefficient.

Lucas Model: HC Dynamics and Returns to Scale¶

\(K_{i}\) and \(H_{i}\) are the inputs of PC and HC used by firm (\(i\)), Produce output (\(Y_{i}\)).
\(\bar{H}\) is the economy's average level of HC.
\(e\) is the parameter that represents strength of the external effect from the \(\bar{H}\) to each firm's productivity.
In the Lucas model, each firm faces constant returns to scale (CRS).
While there are Increasing Returns to Scale (IRS) for the whole economy.
Lucas assumed HC accumulation (\(\dot{H}\)) as:

\[\dot{H} = \frac{dH}{dt} = \gamma(1-u)H\]

where
- \(u\): Time spent working.
- \(\frac{\dot{H}}{H} = \gamma(1-u)\) where \((1-u)\) is the time spent accumulating skill.
HC doesn't grow automatically; it increases when people spend time learning or training.
If individuals spend more time learning, \(u\) is smaller, then \((1-u)\) is larger, leading to \(\dot{H}\) increasing the rate of Growth of HC.